Introduction
In the context of deep neural networks, adversarial examples are imperceptibly perturbed inputs — commonly images — that cause mis-classification. Obtaining networks robust against such perturbations and understanding their existence has received considerable attention within deep learning as well as computer vision. A recent assumption states that adversarial examples can be found off the (low-dimensional) manifold of the data. However, even for small-scale vision datasets such as MNIST [] or Fashion-MNIST [] estimating and manipulating the manifold proves difficult.
In my recent CVPR'19 paper [], I constructed a synthetic dataset, similar to MNIST or Fashion-MNIST, with known manifold: FONTS, see Figure 1. The known manifold allows to study the occurance of adversarial examples in relation to the manifold. For example, the dataset allows to show that adversarial examples indeed leave the manifold, as previously suggested in [], and adversarial examples can be constrained to the manifold, as similar to [].
The dataset and the corresponding code can be found on GitHub:
FONTS on GitHubDataset
FONTS consists of randomly transformed characters "A" to "J". However, the dataset can easily be extended to include more characters (including special characters and digits). The characters are taken from a subset of 1000 (manually cleaned) fonts from Google Fonts where all characters are clearly legible. The letters are rendered (without transformation) into prototype images of the desired resolution — for example, $28 \times 28$ as in MNIST. These prototypes are transformed using a spatial transformer network [] considering translation $[t_1, t_2]$, shear $[\lambda_1, \lambda_2]$, scale $s$ and rotation $r$. These parameters are assembled into an affine transformation matrix
$\left[\begin{array}\cos(r)s - \sin(r)s\lambda_1 & -\sin(r)s + \cos(r)s\lambda_1 & t_1\\ \cos(r)s\lambda_2 + \sin(r)s & -\sin(r)s\lambda_2 + \cos(r)s & t_2\end{array}\right]$.(1)
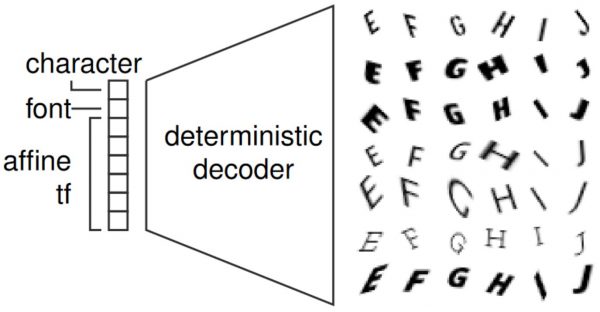
As a result, the generation process is completely differentiable with respect to the transformation parameters, as illustrated in Figure2. Note that the class, meaning the character, and the font are still discrete and solely determined by the prototype image — nevertheless, the generation process can also be made differentiable with respect to font and character. By generating the transformation parameters randomly, and varying their range, datasets of various difficulties and sizes can be created. As font and character are discrete, they are held constant in []; this can be interpreted as modeling font-character manifold.
Figure 2: Illustration of the data generation process used for FONTS. The used decoder is fully differentiable with respect to the affine transformation used as well as font and character; font and character, however, are discrete.
Implementation
The data generation process is implemented in PyTorch and consists of three steps: (a) generating a database of prototype images, meaning the desired characters rendered for all fonts — without any transformations, (b) randomly sampling the transformation parameters of Equation (1) and (c) setting up a decoder to implement the generative process depicted in Figure 2.
For creating a database of prototype images, I followed Deep Fonts: TrueType fonts from Google Fonts are loaded using PIL.ImageFont and the characters "A" to "J" are rendered in a fixed font size. The images are padded and subsequently scaped to $[0,1]$, see Listing 1. The images are stacked such that the database contains, for each font, all $10$ characters:
def read_font(fn):
"""
Read a font file and generate all letters as images.
:param fn: path to font file as TTF
:rtype: str
:return: images
:rtype: numpy.ndarray
"""
# a bit smaller than image size to take transformations into account
size = 28
points = size - size/4
font = PIL.ImageFont.truetype(fn, int(points))
# some fonts do not like this
# https://github.com/googlefonts/fontbakery/issues/703
try:
# https://stackoverflow.com/questions/43060479/how-to-get-the-font-pixel-height-using-pil-imagefont
ascent, descent = font.getmetrics()
(width, baseline), (offset_x, offset_y) = font.font.getsize('A')
except IOError:
return None
data = []
characters = 'ABCDEFGHIJ'
for char in characters:
img = PIL.Image.new('L', (size, size), 255)
draw = PIL.ImageDraw.Draw(img)
textsize = draw.textsize(char, font=font)
draw.text(((-offset_x + size - textsize[0])//2, (-offset_y + size - textsize[1])//2), char, font=font)
matrix = numpy.array(img).astype(numpy.float32)
matrix = 255 - matrix
matrix /= 255.
data.append(matrix)
return numpy.array(data)
Listing 1: Function fo reading a TrueType font file and generating prototype images for all characters.
The remaining latent codes — the transformation parameters of Equation (1) and, optionally, foreground and background color — are sampled randomly. For the dataset distributed together with the paper [], translation, shear, scaling and rotation are sampled uniformly from $[−0.2,0.2]$, $[−0.5,0.5]$, $[0.75,1.15]$, and $[-\frac{\pi}{2},\frac{\pi}{2}]$. The number of samples controls the final size of the dataset. Additionally, allowing large rotations or translations increases the diffculty of the dataset.
Finally, given the latent codes — font, character and transformation parameters — the generative process is implemented as decoder, see Listing 2. The decoder expects a database of prototypes and the number of transformation parameters; for example, $6$ parameters are used for the affine transformation in Equation (1). Then, given the font-character combination and the transformation parameters, the corresponding prototype image is selected and run through a spatial transformer network. This way, the whole process is differentiable with respect to both font-character combination and the used transformation. However, as font and character are inherently discrete, these are usually held constant.
class OneHotDecoder(torch.nn.Module):
"""
The decoder computes, given the font/letter combination (as one/hot vector) and affine transformation parameters,
the resulting images bz first selecting the font/letter from a database and then applying the transformation
through a spatial transformer network.
"""
def __init__(self, database, N_theta, softmax=False, temperature=1):
"""
Initialize decoder.
:param database: database of prototype images
:type database: torch.autograd.Variable
:param N_theta: number of transformation parameters
:type N_theta: int
:param softmax: whether to apply softmax before working with code
:type softmax: bool
:param temperature: temperature of softmax
:type temperature: float
"""
super(OneHotDecoder, self).__init__()
self._theta = None
""" (None or torch.autograd.Variable) Fixed theta if set. """
self._code = None
""" (None or torch.autograd.Variable) Fixed code if set. """
assert len(database.size()) == 3, 'database has to be of rank 3'
self.database = database
self.database.unsqueeze_(0)
""" (torch.autograd.Variable) Database of protoype images. """
self.N_theta = N_theta
""" (int) Number of transformation parameters. """
if softmax:
self.softmax = torch.nn.Softmax(dim=1)
""" (torch.nn.Softmax) Whether to apply softmax. """
self.temperature = temperature
""" (float) Termperature of softmax. """
else:
self.softmax = softmax
""" (bool) Not to use softmax. """
# https://github.com/pytorch/pytorch/issues/4632
#torch.backends.cudnn.benchmark = False
def forward(self, code_or_theta, theta=None):
"""
Wrapper forward function that also allows to call forward on only the code or theta
after setting theta or the code fixed.
The fixed one should not allow gradients.
:param code_or_theta: code or theta
:type code_or_theta: torch.autograd.Variable
:param theta: theta or None
:type theta: torch.autograd.Variable or None
:return: output image
:rtype: torch.autograd.Variable
"""
# Cases:
# 1/ fixed theta
# 2/ fixed code
# 3/ both code and theta give
assert theta is None and self.set_theta is not None \
or theta is None and self.set_code is not None \
or theta is not None
if theta is None:
if self._theta is not None:
return self._forward(code_or_theta, self._theta)
elif self._code is not None:
return self._forward(self._code, code_or_theta)
else:
return self._forward(code_or_theta, theta)
def set_theta(self, theta):
"""
Set fixed theta to use in forward pass.
:param theta: theta
:type theta: torch.autograd.Variable
"""
self._theta = theta
def set_code(self, code):
"""
Set fixed code to use in forward pass.
:param code: code
:type code: torch.autograd.Variable
"""
self._code = code
def stn(self, theta, input):
"""
Apply spatial transformer network on image using affine transformation theta.
:param theta: transformation parameters as 6-vector
:type theta: torch.autograd.Variable
:param input: image(s) to apply transformation to
:type input: torch.autograd.Variable
:return: transformed image(s)
:rtype: torch.autograd.Variable
"""
# theta is given as 6-vector
theta = theta.view(-1, 2, 3)
grid = torch.nn.functional.affine_grid(theta, input.size())
output = torch.nn.functional.grid_sample(input, grid)
return output
def _forward(self, code, theta):
"""
Forward pass, takes a code(s) and generates the corresponding image(s).
:param code: input code(s)
:type code: torch.autograd.Variable
:param theta: input transformation(s)
:type theta: torch.autograd.Variable
:return: output image
:rtype: torch.autograd.Variable
"""
# see broadcasting: http://pytorch.org/docs/master/notes/broadcasting.html
# first computed weighted sum of database with relevant part of code
code = code.view(code.size()[0], code.size()[1], 1, 1)
if self.softmax:
code = self.softmax(code/self.temperature)
image = torch.sum(torch.mul(self.database, code), 1) # 1 x N x H x W and B x N x 1 x 1
image.unsqueeze_(1)
if self.N_theta > 0:
translation_x = theta[:, 0]
if self.N_theta > 1:
translation_y = theta[:, 1]
if self.N_theta > 2:
shear_x = theta[:, 2]
if self.N_theta > 3:
shear_y = theta[:, 3]
if self.N_theta > 4:
scales = theta[:, 4]
if self.N_theta > 5:
rotation = theta[:, 5]
transformation = torch.autograd.Variable(torch.FloatTensor(theta.size()[0], 6).fill_(0))
if common.cuda.is_cuda(theta):
transformation = transformation.cuda()
# translation x
if self.N_theta == 1:
transformation[:, 0] = 1
transformation[:, 4] = 1
transformation[:, 2] = translation_x
# translation y
elif self.N_theta == 2:
transformation[:, 0] = 1
transformation[:, 4] = 1
transformation[:, 2] = translation_x
transformation[:, 5] = translation_y
# shear x
elif self.N_theta == 3:
transformation[:, 0] = 1
transformation[:, 1] = shear_x
transformation[:, 2] = translation_x
transformation[:, 4] = 1
transformation[:, 5] = translation_y
# shear y
elif self.N_theta == 4:
transformation[:, 0] = 1
transformation[:, 1] = shear_x
transformation[:, 2] = translation_x
transformation[:, 3] = shear_y
transformation[:, 4] = 1
transformation[:, 5] = translation_y
# scale
elif self.N_theta == 5:
transformation[:, 0] = scales
transformation[:, 1] = scales * shear_x
transformation[:, 2] = translation_x
transformation[:, 3] = scales * shear_y
transformation[:, 4] = scales
transformation[:, 5] = translation_y
# rotation
elif self.N_theta >= 6 and self.N_theta <= 9:
transformation[:, 0] = torch.cos(rotation) * scales - torch.sin(rotation) * scales * shear_x
transformation[:, 1] = -torch.sin(rotation) * scales + torch.cos(rotation) * scales * shear_x
transformation[:, 2] = translation_x
transformation[:, 3] = torch.cos(rotation) * scales * shear_y + torch.sin(rotation) * scales
transformation[:, 4] = -torch.sin(rotation) * scales * shear_y + torch.cos(rotation) * scales
transformation[:, 5] = translation_y
else:
raise NotImplementedError()
output = torch.clamp(torch.clamp(self.stn(transformation, image), min=0), max=1)
if self.N_theta == 7:
output = torch.mul(output, theta[:, 6].view(-1, 1, 1, 1))
elif self.N_theta == 8:
r = torch.mul(output, theta[:, 6].view(-1, 1, 1, 1))
g = torch.mul(output, theta[:, 7].view(-1, 1, 1, 1))
b = output
output = 1 - torch.cat((
r,
g,
b
), dim=1)
elif self.N_theta == 9:
# view is important as reshape does not allow grads in the cat case
r = torch.mul(output, theta[:, 6].view(-1, 1, 1, 1))
g = torch.mul(output, theta[:, 7].view(-1, 1, 1, 1))
b = torch.mul(output, theta[:, 8].view(-1, 1, 1, 1))
output = 1 - torch.cat((
r,
g,
b
), dim=1)
return output
Listing 2: Generative process implemented as decoder mapping latent code — font, class and transformation — to an image.
Outlook
The decoder in Listing 2 can be used in various ways. In [], I used the decoder to search the latent space for mis-classified examples, resulting in on-manifold adversarial examples in the spirit of []. The decoder, however, can also be used to project any image onto the manifold; this is useful for determining the distance of arbitrary images to the data manifold. I will discuss both use cases in upcoming posts.
- [] David Stutz, Matthias Hein, and Bernt Schiele. Disentangling Adversarial Robustness and Generalization. CVPR, 2019.
- [] Yann LeCun, Leon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to documentrecognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
- [] Han Xiao, Kashif Rasul, Roland Vollgraf. Fashion-MNIST: a Novel Image Dataset for Benchmarking Machine Learning Algorithms. CoRR abs/1708.07747 (2017).
- [] Yang Song, Taesup Kim, Sebastian Nowozin, Stefano Ermon, Nate Kushman. PixelDefend: Leveraging Generative Models to Understand and Defend against Adversarial Examples. ICLR (Poster) 2018.
- [] Justin Gilmer, Luke Metz, Fartash Faghri, Samuel S. Schoenholz, Maithra Raghu, Martin Wattenberg, Ian J. Goodfellow. Adversarial Spheres. ICLR (Workshop) 2018.
- [] Max Jaderberg, Karen Simonyan, Andrew Zisserman, Koray Kavukcuoglu. Spatial Transformer Networks. NIPS 2015: 2017-2025.