RESEARCH
Random Bit Error Robustness
Quick links: MLSys'2021 Paper | MLSys'2021 Code | MLSys'2021 Poster | ICLR'2021 RobustML Short Paper | ICLR'2021 RobustML Short Paper | ICLR'2021 RobustML Short Paper
Abstract
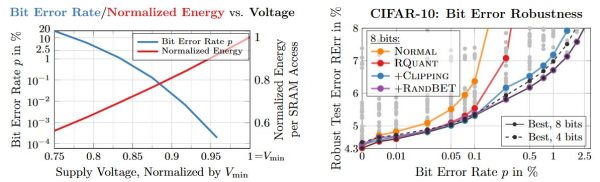
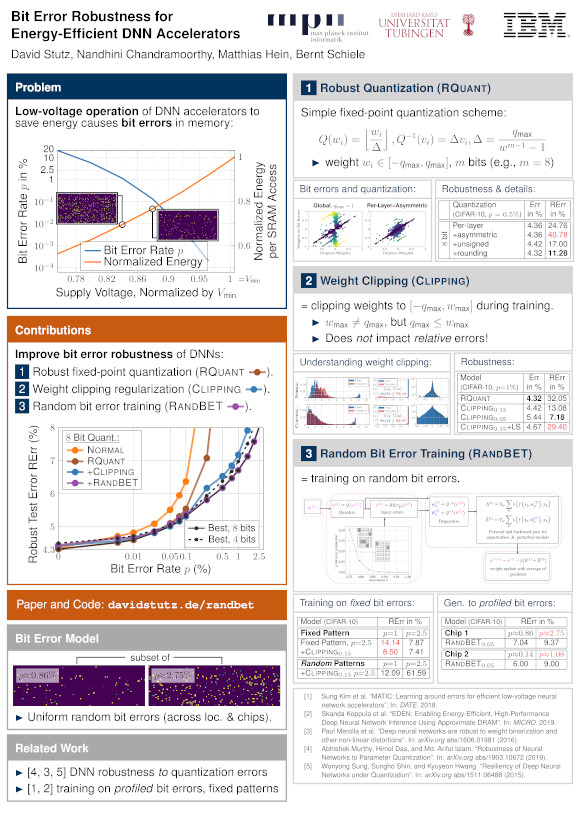
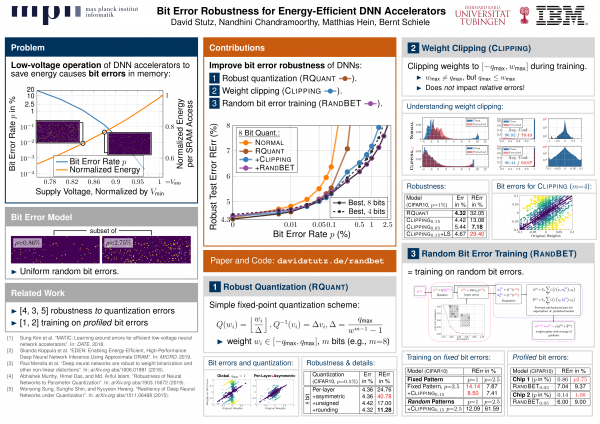
Figure 1: Left: Average bit error rate (blue) and energy (red) against voltage. These are measurements from 32 14nm SRAM arrays of size $512\times64$. Both voltage and energy per SRAM access are normalized to $V_{\text{min}}$, the minimum voltage with error free operation (determined experimentally). SRAM accesses havesignificant impact on the DNN accelerators overall energy consumption, however, reducing voltage causes an exponential increase in bit errors. Right: Robust test error (test error after injecting bit errors) plotted against bit error rates. For $8$ bit quantization, robust fixed-point quantization, training with weight clipping and finally adding random bit error training improves robustness significantly.
Deep neural network (DNN) accelerators received considerable attention in past years due to saved energy compared to mainstream hardware. Low-voltage operation of DNN accelerators allows to further reduce energy consumption significantly, however, causes bit-level failures in the memory storing the quantized DNN weights. In this paper, we show that a combination of robust fixed-point quantization, weight clipping, and random bit error training (RandBET) improves robustness against random bit errors in (quantized) DNN weights significantly. This leads to high energy savings from both low-voltage operation as well as low-precision quantization. Our approach generalizes across operating voltages and accelerators, as demonstrated on bit errors from profiled SRAM arrays. We also discuss why weight clipping alone is already a quite effective way to achieve robustness against bit errors. Moreover, we specifically discuss the involved trade-offs regarding accuracy, robustness and precision: Without losing more than 1% in accuracy compared to a normally trained 8-bit DNN, we can reduce energy consumption on CIFAR-10 by 20%. Higher energy savings of, e.g., 30%, are possible at the cost of 2.5% accuracy, even for 4-bit DNNs.
Paper
The paper is available on ArXiv:
@article{Stutz2020MLSYS,
author = {David Stutz and Nandhini Chandramoorthy and Matthias Hein and Bernt Schiele},
title = {Bit Error Robustness for Energy-Efficient DNN Acceleratorss},
booktitle = {Proceedings of Machine Learning and Systems 2021, MLSys 2021},
publisher = {mlsys.org},
year = {2021},
}
Poster
Code
The code for this paper, including evaluation and pre-trained models, is available on GitHub:
Bit Error Robustness on GitHubFeatures include implementations of various fixed-point quantization schemes, e.g., the proposed robust quantization, training with quantization and weight clipping, and random bit error training. Moreover, the repository includes bit error manipulation tools for torch, supporting int32, int16, int8 and uint8 data types, for CPU and GPU.
News & Updates
Oct 18, 2021. Code for the paper is now available on GitHub
Jul 3, 2021. The paper was selected as distinguished paper at the CVPR'2021 CV-AML Workshop.
Apr 16, 2021. Follow-up work now available on ArXiv.
Jan 21, 2021. The paper has been accepted at MLSys.
Oct 20, 2020. The ArXiv paper has been updated: ArXiv.
June 26, 2020. The paper is available on ArXiv.