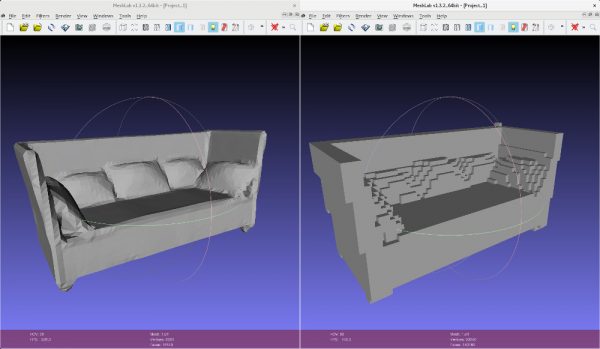
Mesh voxelization is a common problem in 3D vision as triangular meshes are not a suitable shape representation for many algorithms. In deep learning, in particular, occupancy grids and signed distance functions are commonly preferred. Both are defined as dense volumes; for occupancy grids (see Figure 1), each element indicates whether the corresponding voxel is occupied or not — for signed distance functions, each element holds the distance to the nearest surface and the sign is used to distinguish inside and outside. In contrast to occupancy grids, signed distance functions allow to easily reconstruct meshes using marching cubes [].

As part of my master thesis, I implemented a simple but efficient C++ tool for voxelizing watertight meshes into occupancy grids and/or signed distance functions. Here, watertight refers to one, closed surface — this is necessary to reliably determine occupancy. The tool can be found on GitHub:.

The repository also includes Python tools for running marching cubes and several utilities to convert the involved file formats — namely HDF5 files for storing voxelized meshes, and OFF or OBJ files for storing triangular meshes. The results can then be visualized using MeshLab as shown in Figure 1.

The tool is based on:

• the point-to-face distance code from christopherbatty/SDFGen;
• the triangle-ray intersection test by Thomas Möller;
• the triangle-box intersection test by Thomas Möller;
• and the marching cubes implementations of PyMCubes and skimage.

• [] William E. Lorensen and Harvey E. Cline. 1987. Marching cubes: A high resolution 3D surface construction algorithm. SIGGRAPH Comput. Graph. 21, 4 (August 1987), 163-169. DOI: https://doi.org/10.1145/37402.37422.
• [] Z. Wu, S. Song, A. Khosla, F. Yu, L. Zhang, X. Tang and J. Xiao. 3D ShapeNets: A Deep Representation for Volumetric Shapes. CVPR2015..