Introduction
I was planning to have an article series on experimenting with bit errors in quantized deep networks — similar to my article series on adversarial robustness — with accompanying PyTorch code. However, in light of the incredible recent progress in machine learning, I decided to focus on other projects. Nevertheless, I wanted to share the tutorial code I prepared with some pointers for those interested in quantization and bit error robustness. So, in this article, I want to share links to the code, some results and pointers to the relevant literature and background.
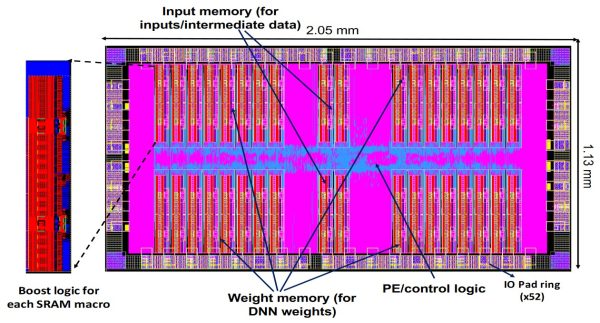
With the incredible interest in deploying deep networks, doing so efficiently on special-purpose hardware becomes more and more important. Often, this involves so-called deep learning accelerators that are explicitly designed for specific architectures and allow space and energy-efficient inference. These chips are often extremely small, as shown in Figure 1, and are comprised of arrays of processing units alongside memory for activations and memory. However, making such chips effective, energy efficient and secure puts additional requirements on the deployed neural networks: networks need to be quantized to few bits per weights and this quantization needs to be reliable to bit errors. The latter are caused by low voltage operation [3] to improve energy efficiency, faulty hardware or can be caused by bit-level attacks on chips.
Our work on bit error robustness [1,2] tackles these requirements on several levels: quanization, regularization and training. The below repository contains PyTorch code demonstrating our work in six steps:
- Fixed-point neural network quantization
- Quantization-aware training yielding 4.5% 4-bit test error on CIFAR10
- Implementing bit operations in Pytorch with CUDA
- Benchmarking bit errors in quantized neural networks
- Training with weight clipping to improve robustness
- Training with random bit errors
- [1] D. Stutz, N. Chandramoorthy, M. Hein, B. Schiele. Bit Error Robustness for Energy-Efficient DNN Accelerators. MLSys, 2021.
- [2] D. Stutz, N. Chandramoorthy, M. Hein, B. Schiele. Random and Adversarial Bit Error Robustness: Energy-Efficient and Secure DNN Accelerators. TPAMI, 2022.
- [3] N. Chandramoorthy, K. Swaminathan, M. Cochet, A. Paidimarri, S. Eldridge, R. V. Joshi, M. M. Ziegler, A. Buyuktosunoglu, and P. Bose, “Resilient low voltage accelerators for high energy efficiency,” in HPCA, 2019.
More details and pointers
101-network-quantization/common/quantization.py with an example in 101-network-quantization/examples.
As naive quantization of pre-trained networks, especially with few bits, leads to significant reduction in accuracy. Thus, common practice is to quantize during training in order to obtain networks robust to the introduced quantization errors. 102-quantization-aware-training/examples/train.py allows to train networks with nearly no accuracy degradation with 8 bit. The below table summarizes some resutls for wide ResNets and SimpleNets with batch normalization (BN) and group normalization (GN):
| Model | Test Error in % |
| WRN-28-10 4-bit BN | 5.83 |
| WRN-28-10 4-bit GN | 6.33 |
| WRN-28-10 8-bit BN | 2.58 |
| WRN-28-10 8-bit GN | 3.17 |
| SimpleNet 4-bit BN | 6.35 |
| SimpleNet 4-bit GN | 5.7 |
| SimpleNet 8-bit BN | 3.65 |
| SimpleNet 8-bit GN | 4.78 |
103-bit-operations/common/torch/bitwise.py uses cffi and cupy to provide bit operations for PyTorch tensors.
Using bit operations in PyTorch, we can easily evaluate the impact of bit errors on quantized networks. Even small bit error rates reduce accuracy quite significantly — especially for models with BN where accuracy quickly reaches chance level. GN-based models, in contrast are more robust. Note that this already includes some of our more robust fixed-point quantization:
| Test Error in % | |||
| Model | No bit errors | 0.1% bit errors | 1% bit errors |
| SimpleNet 4-bit GN | 5.7 | 7.62 | 44.17 |
| SimpleNet 8-bit GN | 4.78 | 6.22 | 34.5 |
A simple but extremely effective regularization scheme to improve bit error robustness is weight clippin: during training, weights are constrained to stay within a limited range $[-w_{\text{max}},w_{\text{max}}]$. While it seems that this improves robustness because it reduces the range of bit errors, as well, it actually turns out that this regularization prefers more "distributed" weights. That is, more weights contribute to the model predictions and this improves robustness to bit errors. Here are some results for the above models:
| Test Error in % | |||
| Model | No bit errors | 0.1% bit errors | 1% bit errors |
| SimpleNet 4-bit GN | 5.7 | 7.62 | 44.17 |
| SimpleNet 4-bit GN with $w_{\text{max}} = 0.1$ | 5.85 | 6.53 | 10.56 |
| SimpleNet 8-bit GN | 4.78 | 6.22 | 34.5% |
| SimpleNet 8-bit GN with $w_{\text{max}} = 0.1$ | 5.72 | 6.43 | 10.92 |
On top of weight clipping, it is also effective to inject bit errors during training to improve robustness. Results for this so-called random bit error training with bit error rate $p$ are included below:
| Test Error in % | |||
| Model | No bit errors | 0.1% bit errors | 1% bit errors |
| SimpleNet 8-bit GN | 4.78 | 6.22 | 34.5% |
| SimpleNet 8-bit GN with $w_{\text{max}} = 0.1$ | 5.72 | 6.43 | 10.92 |
| SimpleNet 8-bit GN with $w_{\text{max}} = 0.1$ and $p = 0.1\%$ | 5.34 | 6.07 | 9.33 |
| SimpleNet 8-bit GN with $w_{\text{max}} = 0.1$ and $p = 1\%$ | 5.67 | 6.27 | 8.53 |