Abstract

Adversarial training (AT), i.e., training on adversarial examples generating on-the-fly, is standard to obtain robust models within a specific threat model, e.g., $L_\infty$ adversarial examples. However, robustness does not generalize to previously unseen attacks such as larger perturbations or other $L_p$ threat models. Furthermore, adversarial training often incurs a drop in accuracy. Confidence-calibrated adversarial training (CCAT) tackles these problems by biasing the network towards low-confidence predictions on adversarial examples. Trained only on $L_\infty$ adversarial examples, CCAT improves robustness against unseen attacks, including $L_2$, $L_1$ and $L_0$ adversarial examples as well as adversarial frames by rejecting low-confidence (adversarial) examples. Additionally, compared to AT, accuracy is improved.

Adversarial Training (AT):

Confidence-Calibrated Adversarial Training (CCAT):

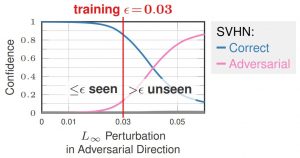
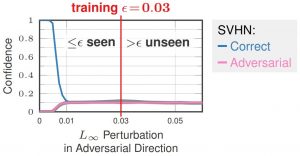
Figure 1: Illustration of how confidence-calibrated adversarial training (CCAT, right) tackles two problems of standard adversarial training(AT, left): poor generalization of robustness to larger perturbations than seen during training, i.e., larger $L_\infty$ adversarial examples than $\epsilon$; and reduced accuracy which might, in part, be due to overlapping $\epsilon$-balls of different classes. In both cases, predicting near uniform distributions helps, as we show for CCAT.

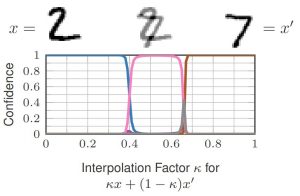
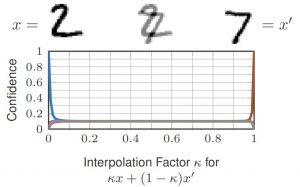
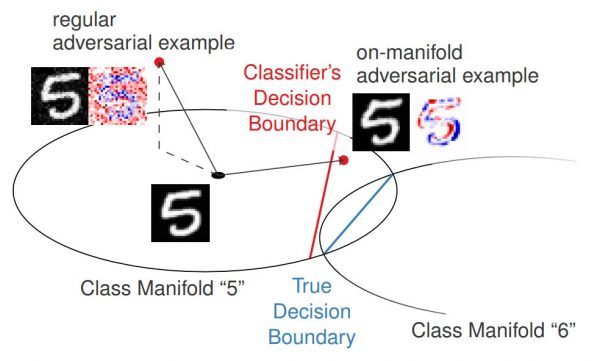
This talk motivates CCAT by the observation that adversarial examples usually leave the underlying manifold of the data, see Figure 2. By encouraging low-confidence predictions on adversarial examples, i.e., off-manifold, the model is biased to extrapolate this behavior to arbitrary regions. The hypothesis is that the robustness of standard AT does not generalize well to unseen attacks as high-confidence predictions cannot be extrapolated to arbitrary regions in a meaningful way. Furthermore, high-confidence predictions are problematic if the $\epsilon$-balls used during training overlap, e.g., for training examples from different classes. Both problems are adressed by predicting uniform confidence within the largest parts of the $\epsilon$-balls, as encouraged by CCAT. Both cases are illustrated in Figure 1.

Finally, the talk also includes three important lessons for properly evaluating CCAT:

1. Use proper evaluation metrics, allowing to reject (adversarial) examples.
2. Define multiple, adaptive adversarial attacks.
3. Use worst-case evaluation, considering multiple attacks with multiple restarts.

Regarding proper evaluation metrics, the talk introduces the confidence-thresholded robust test error which is fully comparable to the standard robust test error while allowing a reject option. Then, it is important to use multiple white- and black-box attacks during evaluation, which are adapted to CCAT by explicitly maximizing the confidence of adversarial examples. Finally, instead of reporting average results per attack, we consider the per-example worst-case adversarial examples for evaluation. Altogether, these three guidelines result in a thorough evaluation of CCAT and a fair comparison to standard AT.

Download

The slides can be downloaded here and the corresponding papers are available on ArXiv:

D. Stutz, M. Hein, B. Schiele. Disentangling Adversarial Robustness and Generalization. CVPR, 2019.

D. Stutz, M. Hein, B. Schiele. Confidence-Calibrated Adversarial Training: Generalizing to Unseen Attacks. ArXiv, 2019.