RESEARCH

Confidence-Calibrated Adversarial Training

Quick links: Paper | Short Paper | Code | BCAI Talk Slides | ICML Slides

Abstract

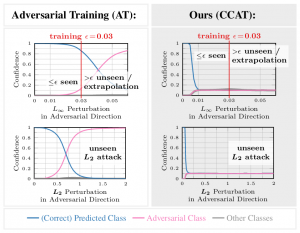
Adversarial training yields robust models against a specific threat model, e.g., $L_\infty$ adversarial examples. Typically robustness does not generalize to previously unseen threat models, e.g., other $L_p$ norms, or larger perturbations. Our confidence-calibrated adversarial training (CCAT) tackles this problem by biasing the model towards low confidence predictions on adversarial examples. By allowing to reject examples with low confidence, robustness generalizes beyond the threat model employed during training. CCAT, trained only on $L_\infty$ adversarial examples, increases robustness against larger $L_\infty$, $L_2$, $L_1$ and $L_0$ attacks, adversarial frames, distal adversarial examples and corrupted examples and yields better clean accuracy compared to adversarial training. For thorough evaluation we developed novel white- and black-box attacks directly attacking CCAT by maximizing confidence. For each threat model, we use $7$ attacks with up to $50$ restarts and $5000$ iterations and report worst-case robust test error, extended to our confidence-thresholded setting, across all attacks.

Paper

The paper is available on ArXiv:

Paper on ArXiv

@inproceedings{Stutz2020ICML,
    author    = {David Stutz and Matthias Hein and Bernt Schiele},
    title     = {Confidence-Calibrated Adversarial Training: Generalizing Robustness to Unseen Attacks},
    booktitle   = {ICML},
    year      = {2020}
}

UDL 2020 Short Paper

A 4-page version of the paper (from UDL 2020) is available below:

Short Paper

Code

The code is available in the following repository:

Code on GitHub

The repository includes installation instructions and documentation.

Features:

• Training procedures for:
  • Adversarial Training []
  • Confidence-Calibrated Adversarial Training
• Various white- and black-box adversarial attacks:
  • PGD [] with backtracking
  • (Reference implementation of PGD without backtracking)
  • Corner Search []
  • Query Limited [] with backtracking
  • ZOO [] with backtracking
  • Adversarial Frames []
  • Geometry []
  • Square []
• Confidence-thresholded evaluation protocol for:
• adverarial examples
• distal adversarial examples
• out-of-distribution examples
• corrupted examples

News & Updates

July 1, 2020. A short version of the paper is accepted at UDL 2020.

July 1, 2020. The revised paper is now available on ArXiv.

June 1, 2020. The paper is accepted at ICML'20.

March 2, 2020. The code is now available on GitHub: davidstutz/confidence-calibrated-adversarial-training.

February 26, 2020. The ArXiv paper was updated, including additional experiments with $L_0$ and $L_1$ adversarial examples as well as adversarial frames.

November 26, 2019. The ArXiv paper was updated, including a more thorough description of the experimental setup and evaluation metrics and presenting additional experiments with $L_0$ and $L_1$ attacks.

October 16, 2019. The paper is available on ArXiv.

References

• [] Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and Vladu, A. Towards deep learning models resistant to adversarial attacks. ICLR, 2018.
• [] Croce, F. and Hein, M. Sparse and imperceivable adversarial attacks. arXiv.org, abs/1909.05040, 2019.
• [] Ilyas, A., Engstrom, L., Athalye, A., and Lin, J. Black-box adversarial attacks with limited queries and information. In ICML, 2018.
• [] Pin-Yu Chen, Huan Zhang, Yash Sharma, Jinfeng Yi, Cho-Jui Hsieh. ZOO: Zeroth Order Optimization Based Black-box Attacks to Deep Neural Networks without Training Substitute Models. AISec@CCS, 2017.
• [] Zajac, M., Zolna, K., Rostamzadeh, N., and Pinheiro, P. O. Adversarial framing for image and video classification. In AAAI Workshops, 2019.
• [] Khoury, M. and Hadfield-Menell, D. On the geometry of adversarial examples. arXiv.org, abs/1811.00525, 2018.
• [] Andriushchenko, M., Croce, F., Flammarion, N., and Hein, M. Square attack: a query-efficient black-box adversarial attack via random search. arXiv.org, 1912.00049, 2019.