Introduction
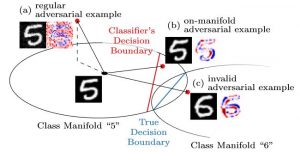
In previous articles, I outlined that adversarial examples, imperceptibly perturbed examples causing mis-classification, tend to leave the underlying data manifold. Similarly, adversarial examples can be constrained explicitly to the data manifold. As illustrated in Figure 1, this results in significantly different noise patterns. On-manifold adversarial examples, for example, correspond to more meaningful manipulation of the image content. As such, I also described them as "hard" test errors.
Figure 1: Illustration of the difference between regular, unconstrained adversarial examples and on-manifold adversarial examples as discussed in [].
In this article, I want to show that training on on-manifold adversarial examples allows to boost generalization significantly. This works as long as the manifold is known or can be approximated well. If the manifold is not known, adversarial training can be applied to adversarial transformations — assuming that invariance to specific transformations is desirable. This approach is similar to many adversarial data augmentation strategies.
This article is part of a series of articles surrounding my recent CVPR'19 paper []:
- FONTS: A Synthetic MNIST-Like Dataset with Known Manifold
- On-Manifold Adversarial Examples
- Adversarial Examples Leave the Data Manifold
On-Manifold Adversarial Training
In the following, I assume that the data manifold is implicitly defined through the data distribution $p(x, y)$ of examples $x$ and labels $y$. A probability $p(x, y) > 0$ means that the example $(x, y)$ is part of the manifold; $p(x, y) = 0$ means the example lies off manifold. With $f$, I refer to a learned classifier, for example a deep neural network, that takes examples $x$ and predicts a label $f(x)$. Then, an on-manifold adversarial example $\tilde{x}$ for $x$ needs to satisfy $f(\tilde{x}) \neq y$ but $p(y|\tilde{x}) > p(y'|\tilde{x})$ for any $y' \neq y$. Note that this condition implies that the optimal Bayes classifier classifies the adversarial example $\tilde{x}$ correctly, but $f$ does not. These adversarial examples can also be thought of as test errors; however, in the following, I will show how to compute them in an "adversarial way".
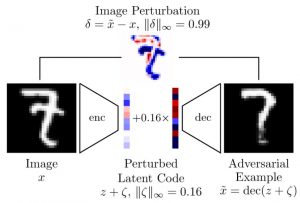
Figure 2: Illustration of on-manifold adversarial examples obtained using a learned variational auto-encoder.
I assume that the data manifold can be modeled using a decoder $\text{dec}$ modeling the generative process $p(x|y, z)$ of an example $x$, given the latent variables $z$ and the label $y$. Here, the latent variables $z$ represent the underlying data manifold. In practice, this could be a learned decoder/generator from a (variational) auto-encoder or generative adversarial network. Then, on-manifold adversarial examples are found by searching the latent space for samples that are mis-classified:
$\max_\zeta \mathcal{L}(f(\text{dec}(z + \zeta)), y)$ such that $\|\zeta\|_\infty \leq \eta$
Here, the cross-entropy loss $\mathcal{L}$ is maximized to cause mis-clssification. The adversarial example, as illustrated in Figure 2, is then obtained as $\text{dec}(z + \zeta)$. Training on on-manifold adversarial examples can be formulated as the following min-max problem, similar to []:
$\min_w \sum_{n = 1}^N \max_{\|\zeta\|_\infty \leq \eta} \mathcal{L}(f(\text{dec}(z_n + \zeta); w), y_n)$(1)
where $w$ are the classifier's weights and $z_n = \text{enc}(x_n)$ are the latent codes of training examples; these can be obtained from the encoder in case of approximating the manifold using (variational) auto-encoders. When an encoder is not accessible, the decoder can still be used by using random $z_n$'s; in this case, training needs to consider clean examples $x_n$ and on-manifold adversarial examples.
Adversarial Transformation Training
Figure 3: Examples from FONTS, a synthetic datasets consisting of randomly transformed letters "A" through "J". In such a case, adversarial transformation training can be used to exploit the known invariances of the dataset (e.g., rotation, scale etc.).
If the manifold is not known but several invariances of the dataset are known, these can be exploited, as well. Assuming that affine transformations are part of the manifold, the decoder $\text{dec}$ in Equation (1) can be replaced by an operator $T(x, t)$ taking an example $x$ and applying the affine transformation $t \in \mathbb{R}^{2 \times 3}$. For example, considering translation $[u, v]$, shear $[\lambda_1, \lambda_2]$, scale $s$ and rotation $r$, the transformation matrix $t$ takes the form:
$\left[\begin{array}\cos(r)s - \sim(r)s\lambda_1 & -\sin(r)s + \cos(r)s\lambda_1 & u\\\cos(r)s\lambda_2 + \sin(r)s & -\sin(r)s\lambda_2 + \cos(r)s & v\end{array}\right]$.
The values allowed for translation, shear, scale and rotation can be chosen in a fashion similar to "random" data augmentation, for which affine transformations are commonly used, as well.
Then, training can be formulated as follows:$\min_w \sum_{n = 1}^N \max_{t \in \mathbb{R}^{2 \times 3}, t \in S} \mathcal{L}(f(T(x_n; \zeta); w), y_n)$(2)
where $S$ represents the set of allowed affine transformations. In practice, $T$ can be implemented as a spatial transformer network, such that $T$ is differentiable. Spatial transformer networks are already implemented in many frameworks such as PyTorch.
Similarities to Data Augmentation. Training on adversarial transformations, as in Equation (2), is similar to the work in [] where training is also applied to adversarially found image transformations. Here, I argued that such an approach can be interpreted as a kind of on-manifold adversarial training. Similarly, there is an increasing body of work on data augmentation using generative adversarial networks [][][][]. In these cases, training examples are generated, but without the goal of being mis-classified. As such, these examples are not necessarily difficult examples.
Results
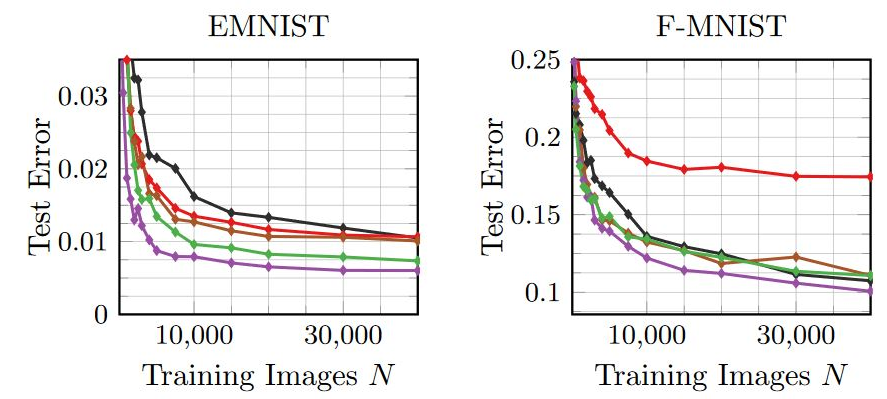
Figure 4: Experimental results on FONTS, MNIST and Fashion-MNIST plotting the obtained test error against the number of training examples $N$ used. I consider normal training, on-manifold adversarial training (either using the true or the learned manifold), adversarial transformation training and a random data augmentation baseline.
Figure 2 shows results for on-manifold adversarial training on FONTS, EMNIST [] and Fashion-MNIST [] in comparison to various baselines. On FONTS, the true manifold is known — read up on the details here. Thus, on-manifold adversarial training is most effective, decreasing test error by multiple percentage points depending on the number of examples $N$ trained on. This can easily be compared to on-manifold adversarial training on a learned manifold, which still improves over normal training, but the improvement is less significant. The difference between both, i.e., on-true-manifold adversarial training and on-learned-manifold adversarial training, is due to the imperfect approximation of the manifold. Also note that on-manifold adversarial training is significantly more effective than "random" data augmentation, especially for small $N$, even if the manifold is approximated.
On EMNIST and Fashion-MNIST, the true manifold is not know. Thus, I compare on-manifold adversarial training using a learned manifold with adversarial transformation training. Note that the transformations used are the same as for random data augmentation. On EMNIST, where the manifold is significantly easier to learn than on Fashion-MNIST, on-manifold adversarial training still reduces test error significantly. On Fashion-MNIST, in contrast, the reduction is insignificant and not consistent across various $N$. Adversarial transformation training, in contrast, is able to reduce test error and also outperform random data augmentation.
Conclusion and Outlook
In this article, I outlined how training on adversarial examples constrained to the data manifold can boost generalization. When the manifold is not known, or cannot reliably be approximated, an adversarial variant of of data augmentation can be used instead. On EMNIST and Fashion-MNIST these strategies allow to reduce test error significantly, especially when training on few training examples. This article illustrates that adversarial examples might, after all, have interesting use cases. In the next and final article of this series, I want to discuss the robustness-accuracy trade-off of "regular" adversarial training, i.e., training on unconstrained adversarial examples.- [] David Stutz, Matthias Hein, Bernt Schiele. Disentangling Adversarial Robustness and Generalization. CVPR 2019.
- [] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, Adrian Vladu. Towards Deep Learning Models Resistant to Adversarial Attacks. ICLR, 2018.
- [] Alhussein Fawzi, Horst Samulowitz, Deepak S. Turaga, andPascal Frossard.
- Adaptive data augmentation for image classification. In ICIP, 2016.
- [] Antreas Antoniou, Amos J. Storkey, and Harrison Edwards. Augmenting image classifiers using data augmentation generative adversarial networks. In ICANN, 2018.
- [] Ekin Dogus Cubuk, Barret Zoph, Dandelion Mane, VijayVasudevan, and Quoc V. Le. Autoaugment: Learning augmentation policies from data. arXiv.org, abs/1805.09501,2018.
- [] Alexander J. Ratner, Henry R. Ehrenberg, Zeshan Hussain, Jared Dunnmon, and Christopher Re. Learning to composedomain-specific transformations for data augmentation. In NIPS, 2017.
- [] Leon Sixt, Benjamin Wild, and Tim Landgraf. Rendergan:Generating realistic labeled data. Frontiers in Robotics and AI, 2018.
- [] Gregory Cohen, Saeed Afshar, Jonathan Tapson, and Andrevan Schaik. EMNIST: an extension of MNIST to handwrit-ten letters. arXiv.org, abs/1702.05373, 2017.
- [] Han Xiao, Kashif Rasul, and Roland Vollgraf. Fashion-MNIST: a novel image dataset for benchmarking machinelearning algorithms. arXiv.org, abs/1708.07747, 2017.