Introduction
The phenomenon of adversarial examples is still poorly understood — including their mere existence. In [], the existence of adversarial examples is attributed to the linearity in state-of-the-art neural networks and the authors of [] speculate that adversarial examples correspond to low-probability regions in the input space rarely seen as part of training or test sets. In [], in contrast, adversarial examples are assumed to lie off the manifold of the underlying data. This so-called manifold assumption is supported by recent empirical results [] indicating that adversarial examples have low probability under the data distribution. Similarly, this assumption has also inspired several recent defenses against adversarial examples [][]. However, as indicated on a simple synthetic dataset in [], adversarial examples can also be found on the data manifold.
Figure 1: Two examples for on-manifold adversarial examples on MNIST and Fashion-MNIST in comparison to "regular", unconstrained adversarial examples.
In this article, I argue that adversarial examples can be constrained to the manifold given a known or approximated manifold. On FONTS, a synthetic dataset from a previous article, the manifold is known by construction allowing to search the manifold explicitly for mis-classified examples. On MNIST and Fashion-MNIST, in contrast, the manifold needs to be approximated. This, can be achieved using VAE-GANs [][]. The resulting adversarial examples look significantly different from "regular" adversarial examples as illustrated in Figure 1.
On-Manifold Adversarial Examples
In the following, I assume that the data manifold is implicitly defined through the data distribution $p(x, y)$ of examples $x$ and labels $y$. A probability $p(x, y) > 0$ means that the example $(x, y)$ is part of the manifold; $p(x, y) = 0$ means the example lies off manifold. With $f$, I refer to a learned classifier, for example a deep neural network, that takes examples $x$ and predicts a label $f(x)$. Then, an on-manifold adversarial example $\tilde{x}$ for $x$ needs to satisfy $f(\tilde{x}) \neq y$ but $p(y|\tilde{x}) > p(y'|\tilde{x})$ for any $y' \neq y$. Note that this condition implies that the optimal Bayes classifier classifies the adversarial example $\tilde{x}$ correctly, but $f$ does not. These adversarial examples can also be thought of as test errors; however, in the following, I will show how to compute them in an "adversarial way".
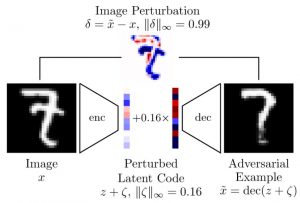
Let the data distribution $p$ be conditioned on latent variables $z$: $p(x, y|z)$. These latent variables reflect the underlying data manifold. In practice, these latent variables are either known (partially) or approximated using any latent variable model. For example, a VAE-GAN can be trained (per class) such that the encoder approximates $\text{enc}(x) \approx p(z|x,y)$ and the decoder approximates $\text{dec}(z) \approx p(x|z, y)$, for fixed $y$. Then, on-manifold adversarial examples can be found efficiently by maximizing
$\max_\zeta \mathcal{L}(f(\text{dec}(z + \zeta)), y)$ such that $\|\zeta\|_\infty \leq \eta$(1)
where $\mathcal{L}$ is the cross-entropy loss and $\eta$ constraints the size of the perturbation $\zeta$ in the latent space. This approach is illustrated in Figure 1; in practice, given $(x,y)$, $z$ is obtained as $z = \text{enc}(x, y)$, Equation (1) is maximized through projected gradient ascent and the perturbed latent code $z + \zeta$ is passed through the decoder to obtain the adversarial example $\tilde{x} = \text{dec}(z + \zeta)$.
Experiments
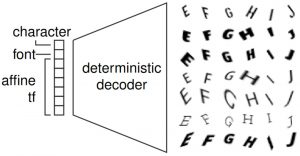
Figure 2: Illustration of the synthetic dataset, FONTS, and the used decoder for computing on-manifold adversarial examples (left) and a depiction of the VAE-GAN used on MNIST/Fashion-MNIST (right).
For experimenting with on-manifold adversarial examples, I created a simple synthetic dataset with known manifold. This means that the conditional data distribution $p(x, y | z)$ is known and, in practice, implemented using a pre-defined (not learned) decoder. Particularly, as illustrated in Figure 2, the latent codes $z$ determine a font type (from Google fonts), a letter (between "A" and "J") and an affine transformation (within reasonable bounds). As a result, the obtained images contain transformed characters "A" to "J" — corresponding to a 10-class problem. The images are MNIST-like, meaning grayscale images of size $28 \times 28$ and nearly binary.
On MNIST [] or Fashion-MNIST [], the manifold is learned using VAE-GANs [][] as also illustrated in Figure 2; as a result, the decoder used in Equation (1) is not perfect. But on MNIST and Fashion-MNIST, I found that VAE-GANs are capable of representing the manifold well enough with a $10$-dimensional latent space.
For solving Equation (1), I used 40 iterations of ADAM with projections onto the $L_\infty$-ball of size $\eta = 0.3$ after each iteration. On FONTS, the manifold is automatically constrained by the allowed transformation parameters (see Figure 2). On MNIST and Fahsion-MNIST, I additionally constrained the latent code to lie within $[-1, 2]^10$ — roughly corresponding to two standard deviation son the latent space.
Figure 3 shows examples of on-manifold adversarial examples in comparison to "regular", unconstrained adversarial examples. On-manifold adversarial examples are also more difficult to find, especially for well-trained models with low test error. On FONTS, on-manifold adversarial examples clearly correspond to transformations of the original test image. This reflects the underlying latent space and also suggests that these on-manifold adversarial examples can be understood as "hard" test examples. When approximating the manifold, the on-manifold adversarial examples might not correspond to the perfect manifold anymore. This can be seen when using an approximate manifold on FONTS. Still, also on MNIST and Fashion-MNIST, on-manifold adversarial exampels correspond to "meaningful" manipulations of the images. For example, digits or characters get thicker or thinner or idnividual lines are removed or added. While these on-manifold adversarial examples are still close to the original images, the change in image space is usually very large — especially in the $L_\infty$ norm.
Conclusion and Outlook
Overall, constraining adversarial examples to the known or approximated manifold allows to find "hard" examples corresponding to meaningful manipulations. Still, the obtained on-manifold adversarial examples are semantically close to the original images, as are "regular" adversarial examples. The difference between both types of adversarial examples implies that regular adversarial examples might not lie on the actual data manifold. In the next article, I will show experimental evidence that this is indeed the case.
- [] David Stutz, Matthias Hein, Bernt Schiele. Disentangling Adversarial Robustness and Generalization. CVPR 2019.
- [] Ian J. Goodfellow, Jonathon Shlens, Christian Szegedy. Explaining and Harnessing Adversarial Examples. ICLR (Poster) 2015.
- [] Christian Szegedy, Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan, Ian J. Goodfellow, Rob Fergus. Intriguing properties of neural networks. ICLR (Poster) 2014.
- [] Thomas Tanay, Lewis D. Griffin. A Boundary Tilting Persepective on the Phenomenon of Adversarial Examples. CoRR abs/1608.07690 (2016).
- [] Yang Song, Taesup Kim, Sebastian Nowozin, Stefano Ermon, Nate Kushman. PixelDefend: Leveraging Generative Models to Understand and Defend against Adversarial Examples. ICLR (Poster) 2018.
- [] Andrew Ilyas, Ajil Jalal, Eirini Asteri, Constantinos Daskalakis, Alexandros G. Dimakis. The Robust Manifold Defense: Adversarial Training using Generative Models. CoRR abs/1712.09196 (2017).
- [] Pouya Samangouei, Maya Kabkab, Rama Chellappa. Defense-GAN: Protecting Classifiers Against Adversarial Attacks Using Generative Models. ICLR (Poster) 2018.
- [] Justin Gilmer, Luke Metz, Fartash Faghri, Samuel S. Schoenholz, Maithra Raghu, Martin Wattenberg, Ian J. Goodfellow. Adversarial Spheres. ICLR (Workshop) 2018.
- [] Anders Boesen Lindbo Larsen, Søren Kaae Sønderby, Hugo Larochelle, Ole Winther. Autoencoding beyond pixels using a learned similarity metric. ICML 2016.
- [] Mihaela Rosca, Balaji Lakshminarayanan, David Warde-Farley, Shakir Mohamed. Variational Approaches for Auto-Encoding Generative Adversarial Networks. CoRR abs/1706.04987 (2017).
- [] Yann LeCun, Leon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to documentrecognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
- [] Han Xiao, Kashif Rasul, Roland Vollgraf. Fashion-MNIST: a Novel Image Dataset for Benchmarking Machine Learning Algorithms. CoRR abs/1708.07747 (2017).