Overview
SEEDS Revised is an implementation of the superpixel algorithm SEEDS proposed in [1] and used for evaluation purposes in [2]. Based on color histograms, an initial superpixel segmentation is iteratively refined. The algorithm is able to generate high-quality superpixel segmentations in near realtime. The implementation is based on OpenCV (compatible with both OpenCV 2 and OpenCV 3), provides thorough documentation and a clean API. Further, a one-parameter variant requiring only the desired number of superpixels is provided:
cv::Mat image = cv::imread(filepath); int superpixels = 800; int iterations = 2; SEEDSRevisedMeanPixels seeds(image, superpixels); seeds.initialize(); seeds.iterate(iterations); // Retrieve labels and put out contour image. int** labels = seeds.getLabels();
The bachelor thesis [2] is available online: Superpixels / SEEDS
You may also go directly to Usage and Parameters instead of learning more about the actual algorithm.
Algorithm
Given an image $I: \{1, \ldots, W\} \times \{1, \ldots, H\} \rightarrow \{0, \ldots, 255\}^3$, the algorithm starts by grouping pixels into blocks of size $w^{(1)} \times h^{(1)}$. These blocks are then further arranged into blocks of $2 \times 2$. This scheme is applied recursively to form a hierarchy of blocks such that blocks at level $l$ have size
$w^{(l)} = w^{(1)} \cdot 2^{l-1}$ and $h^{(l)} = h^{(1)} \cdot 2^{l-1}$.
This is repeated for a total of $L$ levels. Therefore, the number of superpixels is calculated as follows:
$S = \frac{W}{w^{(L)}} \cdot \frac{H}{h^{(L)}}$
where we assume the divisions to be integer divisions. In practice, this means that the number of levels $L$ and the initial block size $w^{(1)} \times h^{(1)}$ need to be dervied from the desired number of superpixels $K$.
The initial superpixel segmentation is refined by exchanging blocks of pixels as well as single pixels between neighboring superpixels. Therefore, let $B_i^{(l)} \subseteq \{1,\ldots, W\}\times\{1,\ldots, H\}$ be a block of pixels at level $l$ and $S_j$ be a superpixel. With $h_{B_i^{(l)}}$ we denote the color histogram of block $B_i^{(l)}$. Then, the similarity of block $B_i^{(l)}$ and superpixel $S_j$ is given by the intersection of the corresponding histograms:
$\cap(h_{B_i^{(l)}}, h_{S_j}) = \sum_{q = 1}^Q \min\{h_{B_i^{(l)}}(q), h_{S_j}(q)\}$
where we assume the histograms to be normalized. Furthermore, the similarity of a single pixel $x_n$ and the superpixel $S_j$ is given by
$h_{S_j}(h(x_n))$
where $h(x_n)$ is the histogram bin of pixel $x_n$. Given this basic framework, algorithm 1 describes a simple implementation of SEEDS.
function SEEDS(
$I$, // Color image.
$w^{(1)} \times h^{(1)}$, // Initial block size.
$L$, // Number of levels.
$Q$ // Histogram size.
)
initialize the block hierarchy and the initial superpixel segmentation
// Initialize histograms for all blocks and superpixels:
for $l = 1$ to $L$
// At level $l = L$ these are the initial superpixels:
for each block $B_i^{(l)}$
initialize histogram $h_{B_i^{(l)}}$
// Block updates:
for $l = L - 1$ to $1$
for each block $B_i^{(l)}$
let $S_j$ be the superpixel $B_i^{(l)}$ belongs to
if a neighboring block belongs to a different superpixel $S_k$
if $\cap(h_{B_i^{(l)}}, h_{S_k}) > \cap(h_{B_i^{(l)}}, h_{S_j})$
$S_k := S_k \cup B_i^{(l)}$, $S_j := S_j - B_i^{(l)}$
// Pixel updates:
for $n = 1$ to $W\cdot H$
let $S_j$ be the superpixel $x_n$ belongs to
if a neighboring pixel belongs to a different superpixel $S_k$
if $h_{S_k}(h(x_n)) > h_{S_j}(h(x_n))$
$S_k := S_k \cup \{x_n\}$, $S_j := S_j - \{x_n\}$
return $S$
As alternative, the similarity of a pixel $x_n$ and a superpixel $S_j$ can be expressed as distance:
$d(x_n, S_j) = \|I(x_n) - I(S_j)\|_2$
where $I(S_j)$ is the mean color of the superpixel $S_j$. This variant of pixel updates is called mean pixel updates [1].
As smooth and compact superpixels are preferrable, van den Bergh et al. [1] introduced a smoothing term: For each pair of pixels $(x_n, x_m)$ (assuming that these pixels belong to different superpixels $S_j$ and $S_k$, respectively), we consider the $3 \times 4$ or $4\times 3$ neighborhood and count the number $N_{n,m,j}$ of pixels belonging to superpixel $S_j$ as well as the number $N_{n,m,k}$ of pixels belonging to superpixel $S_k$. Then, the criterion for pixel updates changes to
$N_{n,m,k}\cdot h_{S_k}(h(x_n)) > N_{n,m,j}\cdot h_{S_j}(h(x_n))$.
This way, we encourage individual pixels to belong to the same superpixel as its neighboring pixels and, thus, enforce smoothness. Of course, this approach can also be applied to mean pixel updates, however, mean pixel updates can be extendend to include an explicit compactness term by using the distance
$d(x_n, S_j) = \|I(x_n) - I(S_j)\|_2 + \beta \|x_n - \mu(S_j)\|_2$, $x_n \in \{1, \ldots, W\} \times \{1, \ldots, H\}$,(∗)
where $\mu(S_j)$ is the mean position of the superpixel $S_j$. The procedure given in algorithm 1 can easily be extended to include the above considerations, see [2].
Complexity
SEEDS runs linear in the total number $N = W\cdot H$ of pixels: SEEDS $\in \mathcal{O}(QTN)$ where $T$ is the number of iterations of block and pixel udpates and $Q$ the histogram size. This can easily be derived when considering to pre-compute the block and superpixel histograms - the histograms can then be updated whenever a block or pixel changes its label.
While the above statement is true, in practice, the runtime of SEEDS does also depend on the number of levels $L$ as well as the block size $w^{(1)} \times h^{(1)}$. Therefore, the runtime only depends indirectly on the number of superpixels $K$ - in particular, the runtime does not scale with $K$.
Usage and Parameters
Compiling
The implementation is based on CMake; e.g. on Ubuntu, CMake can be installed using
$ sudo apt-get install cmake
In addition, OpenCV is required (compatible with both OpenCV 2 and OpenCV 3). See the website for installation details. Then, the implementation can be compiled using
$ git clone https://github.com/davidstutz/seeds-revised.git
$ cd seeds-revised/build
$ cmake ..
$ make
$ ../bin/cli --help
Allowed options:
--help produce help message
--input arg the folder to process, may contain several
images
--bins arg (=5) number of bins used for color histograms
--neighborhood arg (=1) neighborhood size used for smoothing prior
--confidence arg (=0.11) minimum confidence used for block update
--iterations arg (=2) iterations at each level
--spatial-weight arg (=0.25) spatial weight
--superpixels arg (=400) desired number of supüerpixels
--verbose show additional information while processing
--csv save segmentation as CSV file
--contour save contour image of segmentation
--labels save label image of segmentation
--mean save mean colored image of segmentation
--output arg (=output) specify the output directory (default is
./output)
Usage
The implementation provides two classes: SEEDSRevised and SEEDSRevisedMeanPixels where the latter implements the so called mean pixel updates (see above or [2]). The following example shows how to use the SEEDSRevisedMeanPixels class to oversegment a given image:
#include <opencv2/opencv.hpp>
#include "SeedsRevised.h"
#include "Tools.h"
// ...
cv::Mat image = cv::imread(filepath);
// Number of desired superpixels.
int superpixels = 800;
// Number of bins for color histograms (per channel).
int numberOfBins = 5;
// Size of neighborhood used for smoothing term, see [1] or [2].
// 1 will be sufficient, >1 will slow down the algorithm.
int neighborhoodSize = 1;
// Minimum confidence, that is minimum difference of histogram
// intersection needed for block updates: 0.1 is the default value.
float minimumConfidene = 0.1;
// The weighting of spatial smoothing for mean pixel updates - the
// euclidean distance between pixel coordinates and mean superpixel
// coordinates is used and weighted according to:
// (1 - spatialWeight)*colorDistance + spatialWeight*spatialDistance
// The higher spatialWeight, the more compact superpixels are generated.
float spatialWeight = 0.25;
// Number of iterations at each level.
int iterations = 2;
// Instantiate a new object for the given image.
SEEDSRevisedMeanPixels seeds(image, superpixels, numberOfBins, neighborhoodSize, minimumConfidence, spatialWeight);
// Initializes histograms and labels.
seeds.initialize();
// Run block and pixel updates.
seeds.iterate(iterations);
// Save a contour image to the following location:
std::string storeContours = "./contours.png";
// BGR color for contours:
int bgr[] = {0, 0, 204};
// seeds.getLabels() returns a two-dimensional array containing the
// computed superpixel labels.
cv::Mat contourImage = Draw::contourImage(seeds.getLabels(), image, bgr);
cv::imwrite(store, contourImage);
Some details on the parameters:
- image: the image in the form of a
cv::MatinBGRcolor space. - superpixels: number of desired superpixels.
- numberOfBins: number of bins per channel used to calculate the color histograms (see above).
- neighborhoodSize: size of the smoothing window as explained above; $1$ is usually sufficient, greater values will slow down the algorithm and result in smoother superpixels.
- minimumConfidence: minimum difference of histogram intersection required for block updates.
- spatialWeight: only available for
SEEDSRevisedMeanPixels; used to weight the compactness term in (∗).
Qualitative and Quantitative Results
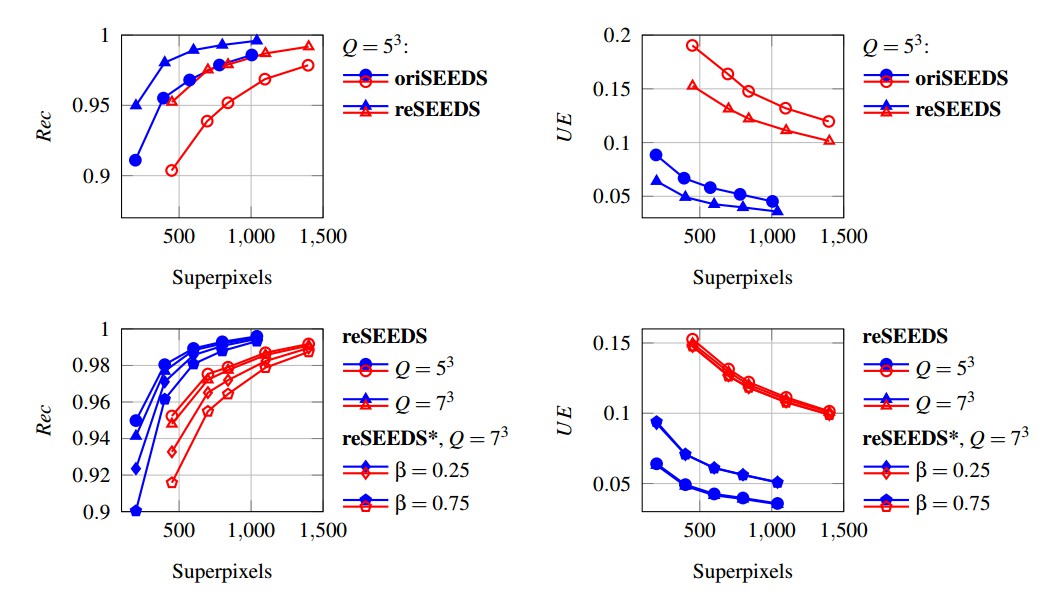
Figure 1 shows superpixel segmentations acquired on images from the Berkeley Segmentation Dataset [3].
Both SEEDS Revised, referred to as reSEEDS, and the original implementation, referred to as oriSEEDS, have been evaluated on training sets of the Berkeley Segmentation Dataset (blue) and the NYU Depth V2 Dataset (red) [4] using an extended version of the Berkeley Segmentation Benchmark [3] which is available on GitHub. Both implementations were evaluated with mean pixel updates and the neighborhood smoothing prior; reSEEDS* additionally uses the compactness term in equation (∗). Figure 2 compares both implementations and shows the influence of the additional compactness term as well as the histogram size. For additional comparison to other state-of-the-art approaches see Superpixels / SEEDS.
Runtime
Table 1 compares the runtime of both implementations on the Berkeley Segmentation Dataset and the Nyu Depth V2 Dataset, see the caption for details.
| Berkeley Segmentation Dataset, $N = 481 \times 321 = 154401$ | |||
|---|---|---|---|
| $K$ | oriSEEDS | reSEEDS | reSEEDS* |
| 200 | 0.14045 | 0.06745 | 0.06955 |
| 400 | 0.23605 | 0.112 | 0.1156 |
| 600 | 0.3354 | 0.14085 | 0.14665 |
| 800 | 0.17285 | 0.08345 | 0.08505 |
| 1040 | 0.21295 | 0.09565 | 0.09985 |
| NYU Depth V2 Dataset, $N = 608 \times 448 = 272384$ | |||
| $K$ | oriSEEDS | reSEEDS | reSEEDS* |
| 450 | 0.30215 | 0.1386 | 0.14455 |
| 700 | 0.41365 | 0.18035 | 0.18795 |
| 840 | 0.21645 | 0.1085 | 0.11398 |
| 1100 | 0.2598 | 0.12515 | 0.13165 |
| 1400 | 0.3068 | 0.141 | 0.14743 |
The runtime of both implementations can be reduced by reducing the number of iterations $T$ as well as the histogram size $Q$. In addition, the neighborhood smoothing prior can be dropped - in particular, as reSEEDS* provides the additional compactness term of equation (∗), the neighborhood smoothing prior can be dropped without reducing compactness or smoothness of superpixels. Table 2 shows the runtime with $T = 1$ and $Q = 3^3$ without using the neighborhood smoothing prior.
| Berkeley Segmentation Dataset, $N = 481 \times 321 = 154401$ | |||
|---|---|---|---|
| $K$ | oriSEEDS | reSEEDS | reSEEDS* |
| 200 | 0.05845 | 0.0292 | 0.02495 |
| 400 | 0.06345 | 0.03525 | 0.03545 |
| 600 | 0.0734 | 0.0401 | 0.05625 |
| 800 | 0.05415 | 0.04245 | 0.03305 |
| 1040 | 0.0625 | 0.0494 | 0.03465 |
| NYU Depth V2 Dataset, $N = 608 \times 448 = 272384$ | |||
| $K$ | oriSEEDS | reSEEDS | reSEEDS* |
| 450 | 0.10583 | 0.0712 | 0.058125 |
| 700 | 0.11395 | 0.09635 | 0.0563 |
| 840 | 0.1128 | 0.073075 | 0.049125 |
| 1100 | 0.11728 | 0.051375 | 0.067825 |
| 1400 | 0.13737 | 0.05395 | 0.06495 |
References
- [1] M. van den Bergh, X. Boix, G. Roig, B. de Capitani, L. van Gool. SEEDS: Superpixels extracted via energy-driven sampling. European Conference on Computer Vision, pages 13–26, 2012.
- [2] D. Stutz. Superpixel Segmentation using Depth Information. Bachelor thesis, RWTH Aachen University, Aachen, Germany, 2014.
- [3] P. Arbeláez, M. Maire, C. Fowlkes, J. Malik. Contour detection and hierarchical image segmentation. Transactions on Pattern Analysis and Machine Intelligence, 33(5):898–916, 2011.
- [4] N. Silberman, D. Hoiem, P. Kohli, R. Fergus. Indoor segmentation and support inference from RGBD images. European Conference on Computer Vision, pages 746–760, 2012.