Abstract
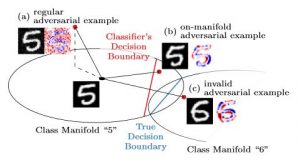
Figure 1: Adversarial examples in the context of the underlying manifold, e.g., class manifolds "5" and "6" on EMNIST, as studied in the paper. Regular adversarial examples result in (seemingly) random noise patterns and usually leave the manifold. However, adversarial examples can also be contrained to the manifold, resulting in more meaningful manipulations of the image content.
Obtaining deep networks that are robust against adversarial examples and generalize well is an open problem. A recent hypothesis even states that both robust and accurate models are impossible, i.e., adversarial robustness and generalization are conflicting goals. In an effort to clarify the relationship between robustness and generalization, we assume an underlying, low-dimensional data manifold and show that: 1. regular adversarial examples leave the manifold; 2. adversarial examples constrained to the manifold, i.e., on-manifold adversarial examples, exist; 3. on-manifold adversarial examples are generalization errors, and on-manifold adversarial training boosts generalization; 4. regular robustness and generalization are not necessarily contradicting goals. These assumptions imply that both robust and accurate models are possible. However, different models (architectures, training strategies etc.) can exhibit different robustness and generalization characteristics. To confirm our claims, we present extensive experiments on synthetic data (with known manifold) as well as on EMNIST, Fashion-MNIST and CelebA.
Paper on ArXiv
@article{Stutz2019CVPR,
author = {David Stutz and Matthias Hein and Bernt Schiele},
title = {Disentangling Adversarial Robustness and Generalization},
booktitle = {IEEE Conference on Computer Vision and Pattern Recognition (CVPR)},
publisher = {IEEE Computer Society},
year = {2019}
}