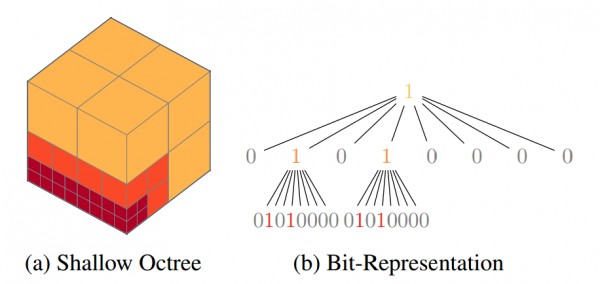
OctNets, illustrated in Figure 1 and proposed by Riegler et al. in [], are octree-based convolutional neural networks intended for efficient learning on 3D data. A C++/CUDA implementation with Torch interface can be found on GitHub at griegler/octnet.
Batch normalization was introduced by Ioffe and Szegedy in [] to address the problem of internal covariate shift. In particular, they discovered that the distribution of network activations may change during training; to prevent internal covariate shift and improve training, batch normalization normalizes the activations over each training batch.
Efficiently implementing batch normalization on octrees is non-trivial because of the variable tree structure; the details will be discussed in detail below. The implementation can be found on GitHub:
OctNet Batch Normalization on GitHubBatch Normalization in OctNets
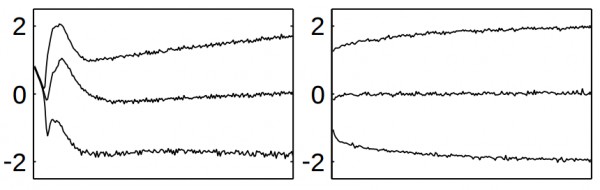
Figure 2 (click to enlarge): A network trained without batch normalization illustrating the observation of covariate shift (left) and a network with batch normalization (right).
Internal covariate shift occurs when the distributions of network activations — for example, of a specific convolutional or fully-connected layer — change significantly during training. This is illustrated in Figure 1 (taken from []). For preventing covariate shift, the activations can be normalized. Batch normalization can be summarized as follows:
Output: Batch-normalized feature maps $\{y_i^{(n)}\}_{n=1}^N$
Algorithm:
$\mu = \frac{1}{M} \frac{1}{B} \sum_b \sum_i x_i^{(b)}$
$\sigma^2 = \frac{1}{M}\frac{1}{B} \sum_b \sum_i (x_i^{(b)})^2 - \mu^2$
$\hat{x}_i^{(b)} = \frac{x_i^{(b)} - \mu}{\sqrt{\sigma^2 + \epsilon}}$
$y_i^{(b)} = \gamma \hat{x}_i^{(b)} + \beta$
Note that this is also referred to as convolutional batch normalization, as all activations within the layers are normalized equally — the parameters $\gamma$ and $\beta$ are also layer-wise. This is important, as regular batch normalization — where each activation is normalized independently — cannot directly be implemented for OctNets. To see this, consider the following examples:
Example. Consider a batch of two octrees with maximum depth 3 (representing volumes of size $8^3$). We can obtain the value $O[i,j,k]$ of voxel $(i,j,k)$ within the volume by traversing the octrees. Additionally, we would have parameters $\gamma_{i,j,k}$ and $\beta_{i,j,k}$ and would need to compute $\mu_{i,j,k} = \frac{1}{2}\left(x_{i,j,k}^{(1)} + x_{i,j,k}^{(2)}\right)$. However, as the tree structure of both octrees need not be identical, we cannot really take advantage of the octree data structure. For example, $O[i,j,k]$ might not be a leaf in octree $1$ — the computation could be shared with $O[i + 1,j,k]$ (and possibly $6$ other voxels). However, in octree $2$, $O[i,j,k]$ and $O[i + 1,j,k]$ might be different. Thus the computation needs to be done for each voxel, $8^3$ in total; this makes the octree structure essentially useless, as not only more computation is required, but also more memory.
Convolutional batch normalization, however avoids this problem by computing the normalization over the full volumes — the full $8^3$ voxels, in our example. This is illustrated in the following, simplified 2D example:
Example. Consider two quadtree (the 2D equivalent of octrees) of maximum depth $3$, as illustrated in Figure 3; the quadtree represents $8^2$ pixels. Then, computing $\mu$ involves summing both over batch samples and pixels. Summing over pixels, per batch sample, can be done very efficiently. For example, considering $0 \leq i,j \leq 2$, $O[i,j]$ is constant — simplifying the computation of $\mu$ as follows:
$\mu = 16 O[0,0] + 4 O[0,4] + 4 O[0,6] + (O[2,4] + O[2,5] + O[3,4] + O[3,5]) + \ldots$
Thus, convolutional batch normalization can be done efficiently on quadtrees as well as octrees.
Implementation
The above example also illustrates how the presented implementation looks in practice. In more detail, the function octree_bn_stat_cpu computing the statistics $\mu$ and $\sigma^2$ is given in the listing below. Normalization, as well as backward passes, can be implemented in a similar manner.
extern "C"
void octree_bn_stat_cpu(const octree* grid, ot_data_t* avgs, ot_data_t* vars) {
const ot_size_t n_blocks = octree_num_blocks(grid);
const ot_size_t channels = grid->feature_size;
// Got through all octrees (there are multiple octrees of max height three).
#pragma omp parallel for
for(int grid_idx = 0; grid_idx < n_blocks; ++grid_idx) {
ot_tree_t* tree = octree_get_tree(grid, grid_idx);
ot_data_t* in_data = octree_get_data(grid, grid_idx);
// If this octree has depth 0 (meaning no splits):
if(!tree_isset_bit(tree, 0)) {
// Mean and variance can be computed by multiplying the value by 8^3
// - the number of voxels.
ot_data_t factor = 8*8*8;
for (int c = 0; c < channels; ++c) {
ot_data_t val = in_data[c];
ot_data_t fval = factor*val; // reduce number of multiplications
#pragma omp atomic
avgs[c] += fval;
#pragma omp atomic
vars[c] += fval*val;
}
}
else {
// If there is at least one split, we check all eight children
// for splits.
int bit_idx_l1 = 1;
for(int bdl1 = 0; bdl1 < 2; ++bdl1) {
for(int bhl1 = 0; bhl1 < 2; ++bhl1) {
for(int bwl1 = 0; bwl1 < 2; ++bwl1) {
// Again, check for split; if not, the factor is 4^3 this time.
if(!tree_isset_bit(tree, bit_idx_l1)) {
int data_idx = tree_data_idx(tree, bit_idx_l1, channels);
ot_data_t factor = 4*4*4;
for (int c = 0; c < channels; ++c) {
ot_data_t val = (in_data + data_idx)[c];
ot_data_t fval = factor*val; // reduce number of multiplications
#pragma omp atomic
avgs[c] += fval;
#pragma omp atomic
vars[c] += fval*val;
}
}
else {
// Again, go through all children and repeat.
int bit_idx_l2 = tree_child_bit_idx(bit_idx_l1);
for(int bdl2 = 0; bdl2 < 2; ++bdl2) {
for(int bhl2 = 0; bhl2 < 2; ++bhl2) {
for(int bwl2 = 0; bwl2 < 2; ++bwl2) {
// Check for split at the last (possible) split level;
// Factor is 2^3 this time.
if(!tree_isset_bit(tree, bit_idx_l2)) {
int data_idx = tree_data_idx(tree, bit_idx_l2, channels);
ot_data_t factor = 2*2*2;
for (int c = 0; c < channels; ++c) {
ot_data_t val = (in_data + data_idx)[c];
ot_data_t fval = factor*val; // reduce number of multiplications
#pragma omp atomic
avgs[c] += fval;
#pragma omp atomic
vars[c] += fval*val;
}
}
else {
// Lowest level, no splits possible anymore.
int bit_idx_l3 = tree_child_bit_idx(bit_idx_l2);
for(int bdl3 = 0; bdl3 < 2; ++bdl3) {
for(int bhl3 = 0; bhl3 < 2; ++bhl3) {
for(int bwl3 = 0; bwl3 < 2; ++bwl3) {
int data_idx = tree_data_idx(tree, bit_idx_l3, channels);
for (int c = 0; c < channels; ++c) {
ot_data_t val = (in_data + data_idx)[c];
#pragma omp atomic
avgs[c] += val;
#pragma omp atomic
vars[c] += val*val;
}
bit_idx_l3++;
}
}
}
}
bit_idx_l2++;
}
}
}
} // else L1
bit_idx_l1++;
} // for bwl1
} // for bhl1
} // for bdl1
} // else L0
} // for grid_idx
const ot_size_t M = 8*grid->grid_depth*8*grid->grid_height*8*grid->grid_width*grid->n;
for (int c = 0; c < channels; ++c) {
avgs[c] /= M;
vars[c] /= M;
vars[c] -= avgs[c]*avgs[c];
}
}
The remaining code can be found in core/src/bn.cpp; the above example, however, illustrates how batch normalization can easily be implemented on octrees.
Usage and Examples
The repository also provides a Torch/LUA example for using OctNets with batch normalization. The example is located in example/02_classification_3d/ and implements a simple classification network on a 3D toy dataset which can be generated on-the-fly. The model is defined as follows:
model = nn.Sequential() model:add(oc.OctreeConvolution3x3x3(1, 8, 'avg')) model:add(oc.OctreeBatchNormalization(8)) model:add(oc.OctreeBatchNormalizationSS(8)) model:add(oc.OctreeReLU(true)) -- ...
- [] Gernot Riegler, Ali Osman Ulusoy, Andreas Geiger: OctNet: Learning Deep 3D Representations at High Resolutions. CVPR 2017: 6620-6629.
- [] Sergey Ioffe, Christian Szegedy: Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. ICML 2015: 448-456