Introduction
In the previous articles of this series, I wrote about the difference of regular, unconstrained adversarial examples and so-called on-manifold adversarial examples, explicitly constrained to the underlying manifold of the data. Most importantly, I argued that regular adversarial examples indeed leave the data manifold, as commonly assumed in the literature [][][]. This implies that the vulnerability to adversarial examples might be due to the neural network not "knowing" how to behave off-manifold. Adversarial training [], that is training on adversarial examples generated on-the-fly, addresses this problem by explicitly treating adversarial examples as part of the learning problem. Intuitively, this means that the manifold is extended to also include adversarial examples.
In this article, I present experiments showing that adversarial training has higher sample complextiy. In practice, this is commonly observed by an apparent robustness-accuracy trade-off: on a dataset of fixed size, adversarial training will improve robustness at the cost of reduced accuracy. On datasets such as Cifar10 or Cifar100 [], the drop in accuracy can be significant. This trade-off is sometimes argued to be inherent []. However, by considering a synthetic dataset with possibly unlimited dataset, I show that this trade-off is not due to an inherent trade-off but caused by a higher sample complexity of adversarial training.
This article is part of a series of articles surrounding my recent CVPR'19 paper []:
- FONTS: A Synthetic MNIST-Like Dataset with Known Manifold
- On-Manifold Adversarial Examples
- Adversarial Examples Leave the Data Manifold
- On-Manifold Adversarial Training for Boosting Generalization
Adversarial Training
Adversarial training can be formulated as a min-max learning problem:
$\min_w \mathbb{E}[\max_{\|\delta\|_\infty\| \leq \epsilon} \mathcal{L}(f(x + \delta; w), y)]$
where $f(\cdot; w)$ is the model with parameters $w$ that are learned, $(x,y)$ are image-label pairs and the inner maximization problem corresponds to computing adversarial examples with perturbation $\delta$ constrained to a $L_\infty$-ball of size $\epsilon$. In practice, for each mini-batch, adversarial examples are computed and used for updating the weights. In order to control the robustness-accuracy trade-off described above, some works [] divide each mini-batch into $50\%$ clean and $50\%$ adversarial examples. This variant effectively optimizes
$\min_w \left((1 - \lambda)\mathbb{E}[\max_{\|\delta\|_\infty\| \leq \epsilon} \mathcal{L}(f(x + \delta; w), y)] + \lambda\mathbb{E}[\mathcal{L}(f(x; w), y)]\right)$.
Training with $50\%$/$50\%$ clean/adversarial examples amounts to $\lambda = 0.5$. However, larger $\lambda \in [0,1]$ puts more weight on clean accuracy.
Datasets
In the literature, adversarial training is usually benchmarked on datasets of fixed size, for example MNIST [], Fashion-MNIST [] or Cifar10/100. For a fixed number of training examples, adversarial training will likely reduce accuracy compared to "normal" training. In this article, instead, I want to show experiments when training with varying numbers of training examples. To this end, I will use FONTS [], a synthetic MNIST-like dataset of randomly transformed characters "A" to $J$ with potentially unlimited number of training examples. While MNIST is comparably simple, with expected test errors of below $1\%$ even for few training examples, FONTS was constructed to be more difficult, with expected test errors between $4\%$ and $10\%$.
Adversarial Training Requires More Training Examples
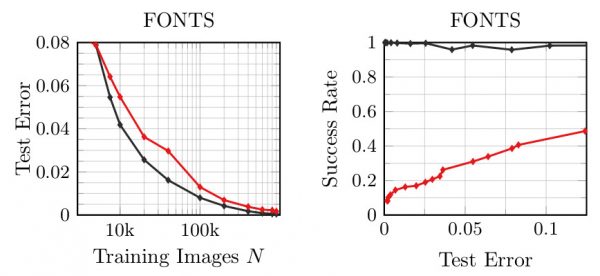
Figure 1: Experimental results on FONTS with varying number of training examples $N$. Left: Test error for adversarial (red) and normal training (black); right: success rate plotted against the test error.
Figure 1 shows test error and success rate of regular adversarial examples on FONTS where the x-axis varies the number of examples used for training. Here, success rate is the fraction of the first $1000$ test examples that were classified correctly and attacked successfully within an $L_\infty$-constraint of $\epsilon = 0.3$. For an arbitrary but fixed number of training examples (comparing vertically), adversarial training in red will always have higher test error than normal training in black. However, success rate is reduced; this means that robustness is increased. However, comparing horizontally for an arbitrary but fixed (desired) test error, Figure 1 shows that adversarial training "just" required roughly $2$ to $2.5$ times more training examples to obtain the same test error while increasing robustness. Overall, this very simple experiments illustrates the increased sample complexity of adversarial training. Moreover, this result suggests that there might not be an inherent trade-off between robustness and accuracy for many interesting problems.
Conclusion
In this article, I used a simple experiment to show that adversarial training exhibits higher sample complexity than normal training. In practice where models are usually trained using all available training examples, this leads to a reduced accuracy of adversarial training compared to normal training. This observation motivated the idea of an inherent robustness-accuracy trade-off of adversarial training. However, comparing adversarial training and normal training on a synthetic dataset with possibly unlimited training data shows that adversarial training can obtain the same accuracy as normal training if more training examples are available. This means that adversarial training might have higher sample complexity than normal training.
- [] David Stutz, Matthias Hein, Bernt Schiele. Disentangling Adversarial Robustness and Generalization. CVPR 2019.
- [] Justin Gilmer, Luke Metz, Fartash Faghri, Samuel S.Schoenholz, Maithra Raghu, Martin Wattenberg, and Ian Goodfellow. Adversarial spheres. ICLR Workshops, 2018.
- [] Thomas Tanay and Lewis Griffin. A boundary tilting persepective on the phenomenon of adversarial examples. arXiv.org, abs/1608.07690, 2016.
- [] Yang Song, Taesup Kim, Sebastian Nowozin, Stefano Ermon, and Nate Kushman. Pixeldefend: Leveraging generative models to understand and defend against adversarial examples. ICLR, 2018.
- [] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, Adrian Vladu. Towards Deep Learning Models Resistant to Adversarial Attacks. ICLR, 2018.
- [] Dimitris Tsipras, Shibani Santurkar, Logan Engstrom, Alexander Turner, Aleksander Madry. Robustness May Be at Odds with Accuracy. ICLR (Poster) 2019.
- [] Christian Szegedy, Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan, Ian Goodfellow, and Rob Fergus. Intriguing properties of neural networks. arXiv.org, abs/1312.6199, 2013.
- [] LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. Gradient-based learning applied to document recognition. Proc. of the IEEE, 86(11):2278–2324, 1998.
- [] Han Xiao, Kashif Rasul, and Roland Vollgraf. Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms. arXiv.org, abs/1708.07747, 2017.
- [] Krizhevsky, A. Learning multiple layers of features from tiny images. Technical report, 2009.