Qi et al. introduce PointNet, a network architecture able to learn directly from unordered point clouds. The architecture is based on several key ideas and they provide experiments tackling 3D object classification and 3d segmentation.

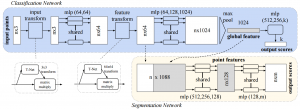
The high level architecture is shown in Figure 1 where both a classification and a segmentation network is shown (which share layers to some extend). The first idea is that a general function operating on a point set can be approximated by transforming the points individually and then applying a symmetric function on the transformed points:

$f(\{x_1,\ldots,x_n\}) \approx g(h(x_1),\ldots,h(x_n))$

Here, $f$ denotes the function to be approximated, $h$ is a point wise transformation and $g$ a symmetric function. In their case, $h$ is computed using a simple multi-layer perceptron (see Figure 1, referred to as "mlp") and $g$ is the max pooling operation. For segmentation, the second idea is to fuse both local information as well as global information. To this end, as illustrated in Figure 1, the input to the segmentation network consists of the set of transformed point features (in this case $n \times 64$ features) concatenated by the global feature extracted by the classification network using the max pooling operation. Finally, they jointly learn an alignment network on the input points as well as on the feature points ($n \times 3$ input and $n \times 64$ features in Figure 1). Therefore, they learn an affine transformation using a mini-network and directly apply this transformation to the coordinates or features of the points. To make training feasible (especially for the transformation network on the $n \times 64$ features) a regularizer is introduced:

$L_{\text{reg}} = \|I - AA^T\|_F^2$

where the transformation matrix is regularized to be close to orthogonal.

In a theoretical section, they show that the proposed network can act as a universal approximator (as known from general multi-layer perceptrons). To this end, they show that for each continuous function $f$ and for all errors $\epsilon$ there exist a function $h$ and a symmetric function $g = \gamma \circ \max$ such that

$\left| f(S) - \gamma(\max\{h(x_i)\})\right| < \epsilon$

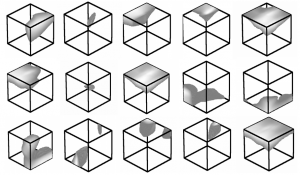
In experiments they show that the proposed classification network demonstrates state-of-the-art performance in 3D object classification. They further show promising results in 3D semantic segmentation and also discuss several visualizations of the learned network. For example, Figure 2 shows points where the per point function $h$ (i.e. the computed values in the $1024$ dimensional per-point features in Figure 1) exceeds $0.5$; $15$ random per-point functions $h$ are displayed.

Fan et al. introduce point set generating networks – closely related and based on the PointNet idea []. Tackling the problem of single-image 3D reconstruction, they make two major contributions: defining and discussing suitable reconstruction losses allowing to compare two point clouds; and extending the chosen loss to account for uncertainty. In general, they consider a model of the form

$S = G(I, r; \theta)$

where $S$ is the predicted point cloud, $I$ the input image (e.g. with depth) and $r$ a random variable perturbing the input (e.g. $r \sim \mathcal{N}(0,1)$). The vanilla (baseline) model they propose is illustrated in Figure 1.

Regarding the loss, they propose both the Chamfer distance and the Earth Mover Distance:

$D_{CD}(S_1, S_2) = \sum_{x \in S_1} \min_{y \in S_2} \|x – y\|_2^2 + \sum_{y \in S_2} \min_{x \in S_1} \|x – y\|_2^2$

$D_{EMD}(S_1, S_2) = \min_{\phi} \sum_{x \in S_1} \|x - \phi(x)\|_2$

where, for the Earth Mover Distance, $\phi$ is a bijection between the two point sets which essentially solves the assignment problem. For this, they use an approximation for efficiency.

However, the uncertainty (also modeled through the random variable $r$) is not taken into account. Therefore, they adapt the loss to state the overall optimization problem over the parameters $\theta$ of the model as

$\min_\theta \sum_k \min_{r_j \sim N(0,1), 1 \leq j \leq n} \{d(G(I_k, r_j;\theta), S_k)\}$

where $S_k$ is the ground truth corresponding to image $I_k$. The loss is called the Min-of-N loss as it considers the minimum of $n$ randomized predictions.

They provide experimental results on various tasks, including shape completion from RGBD images where qualitative results can be found din Figure 2.

• [] Charles Ruizhongtai Qi, Hao Su, Kaichun Mo, Leonidas J. Guibas. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. CoRR abs/1612.00593, 2016.