RESEARCH
Superpixel Benchmark (2014)
A lot of superpixel algorithms have been proposed in the last decade. Therefore, it is difficult to select appropriate approaches for specific applications. This page presents results obtained during my bachelor thesis at RWTH Aachen University: a qualitative and quantitative comparison of several state-of-the-art superpixel algorithms.
Quick links: Bachelor Thesis | GCPR Paper | GCPR Poster | BibTex | Source Code and Data
Update. Check out a more comprehensive comparison of superpixel algorithms here.
Update. The results have been published at the Young Researcher Forum of GCPR 2015!
Paper (∼ 2.7MB)Poster (∼ 7.2MB)
The final publication is available at link.springer.com. Details can be found below.
Update. LaTeX source of the bachelor thesis and the slides, as well as the code for evaluation is now available on GitHub.
Update. Superpixels Revisited (GitHub) bundles several of the evaluated superpixel algorithms in a single library.
Update. An updated version of the thesis is available below. Thanks to Rudolf Mester, a mistake in figure 7.11 on page 57 was corrected.
Overview
The main contribution of this work is a qualitative and quantitative comparison of state-of-the-art superpixel algorithms. Furthermore, the thesis resulted in a new implementation of the superpixel algorithm proposed in [1], called SEEDS. For the quantitative evaluation, the Berkeley Segmentation Benchmark [2] was extended to include several measures suited for assessing superpixel algorithms: Among others, these measures are the Undersegmentation Error [26] and the Achievable Segmentation Accuracy [15]. A list of the evaluated superpixel algorithms can be found in the next section. All algorithms where evaluated on both the Berkeley Segmentation Dataset [2] and the NYU Depth V2 Dataset [6].
Summary of contributions:
- An extended version of the Berkeley Segmentation Benchmark [2] suited for evaluating superpixel algorithms: extended Berkeley Segmentation Benchmark.
- Extensive quantitative evaluation of the individual algorithms on training sets and a comparison on test sets.
The thesis in .pdf format is available below. In addition, LaTeX source as well as source code for the algorithms evaluated below (including the extended version of the Berkeley Segmentation Benchmark [2]) are available on GitHub:
Download and Citing
The GCPR 2015 paper as well as the corresponding poster can be downloaded below. Note that the final publication is available at link.springer.com.
Paper (∼ 2.7MB)Poster (∼ 7.2MB)
@incollection{Stutz:2015,
title = {Superpixel Segmentation: An Evaluation},
author = {Stutz, David},
year = {2015},
isbn = {978-3-319-24946-9},
booktitle = {Pattern Recognition},
volume = {9358},
series = {Lecture Notes in Computer Science},
editor = {Gall, Juergen and Gehler, Peter and Leibe, Bastian},
doi = {10.1007/978-3-319-24947-6_46},
publisher = {Springer International Publishing},
pages = {555 -- 562},
}
The original bachelor thesis is available below:
Due to the extensive amount of evaluation data, appendix B is available separately.
Thesis (∼57MB)Appendix B (∼98MB)
@misc{Stutz:2014,
author = {David Stutz},
title = {Superpixel Segmentation using Depth Information},
month = {September},
year = {2014},
institution = {RWTH Aachen University},
address = {Aachen, Germany},
howpublished = {http://davidstutz.de/},
}
Superpixel Algorithms
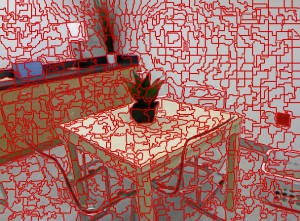
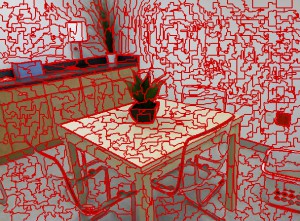
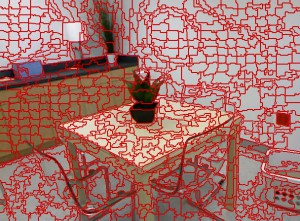
An overview over available superpixel algorithms is given in figure 1.
The following superpixel algorithms have been evaluated in the course of the thesis. Here, the new implementation of SEEDS [1] is called SEEDS Revised.
For each algorithm, a link to the evaluated implementation is provided. In addition, the results obtained on the test sets of the Berkeley Segmentation Dataset (BSDS500) [2] and the NYU Depth V2 Dataset (NYUV2) [6] are available for download. Click an algorithm's name to view details.
The normalized cuts algorithm was originally proposed in 2000 by Shi et al. [8] for the task of classical segmentation. In 2003, Ren et al. used normalized cuts as integral component for the very first superpixel algorithm. The normalized cuts algorithm is a graph based algorithm using graph cuts to optimize a global energy function.
Proposed in 2004, this is another graph based approach which was originally not intended to generate superpixel segmentations. The algorithm is based on a predicate describing whether there is evidence for a boundary between to segments. Using an initial segmentation where each pixel is its own segment, the algorithm merges segments based on this predicate.
Proposed four years later in 2008, QS can be categorized as gradient ascent method and is a mode-seeking algorithm. It was originally not intended as superpixel algorithm. After estimating a density $p(x_n)$ for each pixel $x_n$, the algorithm follows the gradient of the density to assign each pixel to a mode. The modes represent the final segments.
In 2009, this was one of the first algorithms explicitly designed to obtain superpixel segmentations (that is, after [12]). Turbopixels is an algorithm inspired by active contours. After selecting initial superpixel centers, each superpixel is grown by the means of an evolving contour.
Proposed in 2010, this algorithm is often used as baseline [8,9] and is particular interesting because of its simplicity. SLIC implements a local $K$-means clustering to generate a superpixel segmentation with $K$ superpixels. Therefore, SLIC can be categorized as gradient ascent method.
Both proposed in [14], these are two additional graph based methods. In addition, both approaches are defined on grayscale images. Initially, the image is covered by overlapping squares such that each pixel is covered by several squares. Each square represents a superpixel and each pixel can get assigned to one of the overlapping squares. The assignment for each pixel is computed using $\alpha$-expansion.
This algorithm is another graph based method and was proposed in 2011. An objective function based on the entropy rate of a random walk on the graph $G$ corresponding to the image is proposed. The energy function consists of a color term, encouraging superpixels with homogeneous color, and a boundary term, favoring superpixels of similar size.
Proposed in 2011, this algorithm is comparable to CS and CIS. First, the image is overlayed by overlapping vertical and horizontal strips such that each pixel is covered by exactly two vertical strips and two horizontal strips. This way, considering only the horizontal strips, each pixel is either labeled $0$ or $1$. The assignment is computed using max-flow (see [16] for details). Together, the labels corresponding to the horizontal strips and the labels of the vertical strips form a superpixel segmentation.
Proposed in 2013, this algorithm can be categorized as gradient ascent method. Based on an initial superpixel segmentation, the superpixels are refined by exchanging blocks of pixels and single pixels between neighboring superpixels using color histograms.
Proposed in 2012, this is the first algorithm utilizing depth information to improve the generated superpixel segmentation. Although similar to SLIC, this algorithm heavily relies on depth information for choosing the initial superpixel centers and the actual $K$-means clustering.
TPS aims to generate a superpixel segmentation representing a regular grid topology, that is the superpixels can be arranged in an array where each superpixel has a consistent, ordered position [13]. Therefore, after choosing a set of pixels as initial grid positions, these positions are shifted to the maximum edge positions based on a provided edge map. Then, the positions define an undirected graph based on the relative positions. Neighboring grid positions are connected using shortest paths in a weighted graph, where the weight between two pixels is inverse proportional to the edge probability of those pixels.
This approach, proposed in 2013, represents a statistical approach to the task of superpixel segmentation where the image $I$ is assumed to be a result of multiple stochastic processes. Actually, the value of pixel $x_n$ in channel $c$ is thought to be an outcome of a stochastic process specific to the corresponding superpixel. An energy is derived which is optimized using a hill-climbing algorithm.
This is the first algorithm generating supervoxels by oversegmenting a point cloud. VCCS is similar to SLIC and DASP. Based on a 26-adjacency graph constructed from a voxelized point cloud, local $K$-means clustering is applied to form supervoxels. However, in contrast to SLIC, connectivity is ensured by using breadth-first search as basis for $K$-means clustering.
For the remaining superpixel algorithms an evaluation was not possible:
Benchmark
For evaluation, the Berkeley Segmentation Benchmark [2] was extended to include the following measures:
- Undersegmentation Error [26];
- Achievable Segmentation Accuracy [15];
- Compactness [27];
- Explained Variation [18];
- Sum-Of-Squared Error;
For details, see the corresponding papers. In addition, Boundary Recall was used for evaluation.
Datasets and Parameter Optimization
All algorithms were evaluation on the Berkeley Segmentation Dataset [2] and the NYU Depth V2 Dataset [6]. Both datasets provide ground truth segmentations. For the Berkeley Segmentation Dataset the provided validation ($100$ images) and test set ($200$ images) were used. For the NYU Depth V2 Dataset, a custom split was used: $200$ images were selected to form a validation set; $400$ images were selected to form a test set. The images of the NYU Depth V2 Dataset were cropped by $16px$ at each side and the ground truth was pre-processed - the corresponding code is available on GitHub.
Parameters have been optimized on the validation sets with respect to both Boundary Recall and Undersegmentation Error. Note that the parameter space was not searched entirely.
Qualitative Comparison
Note that oriSEEDS refers to the original implementation of SEEDS while reSEEDS refers to the revised implementation of SEEDS.
Quantitative Comparison
The plots below show the quantitative results of the algorithms on the Berkeley Segmentation Dataset (BSDS500) and the NYU Depth V2 Dataset (NYUV2). Unfortunately, due to the prohibitive runtime of NC the results on the smaller validation set of the Berkeley Segmentation Dataset and the training set of the NYU Depth V2 Dataset are shown. In addition, we were not able to evaluate CIS and TPS with respect to Sum-of-Squared Error and Explained Variation.
In addition, the runtime of the algorithms is shown. Note that images from the Berkeley Segmentation Dataset have $N = 481 \cdot 321 = 154401$ pixels while images from the NYU Depth V2 Dataset have $N = 608 \cdot 448 = 272384$ pixels (images from the NYU Depth V2 Dataset have been pre-processed and cropped, see the thesis for details).
Note that oriSEEDS refers to the original implementation of SEEDS while reSEEDS refers to the revised implementation of SEEDS. In addition, SEEDS3D uses 3D information to enhance superpixel segmentation.
Note that the below visualizations, based on nv.d3.js, requires JavaScript to be activated and should be viewed with a recent browser (for example Firefox or Chrome). Alternative visualizations are available in the bachelor thesis.
BSDS500
NYUV2
Conclusion
In conclusion, the observation can be summarized in three important observations:
- The revised implementation of SEEDS, available on GitHub, is able to compete with all evaluated algorithms both in terms of performance and runtime. Actually, providing near realtime, while achieving state-of-the-art performance, it is one of the fastest algorithms available.
- Using depth information for superpixel segmentation does not provide a significant increase in performance. This observation is supported by several algorithms using depth information.
- Several superpixel algorithms provide state-of-the-art performance in runtime. Therefore other aspects become more important: the availability of implementations, ease-of-use, visual quality and especially runtime.
Acknowledgements
This work is part of a bachelor thesis written at the Computer Vision Group at RWTH Aachen University supervised by Alexander Hermans and Bastian Leibe.
References
- [1] M. van den Bergh, X. Boix, G. Roig, B. de Capitani, L. van Gool. SEEDS: Superpixels extracted via energy-driven sampling. European Conference on Computer Vision, pages 13–26, 2012.
- [2] P. Arbeláez, M. Maire, C. Fowlkes, J. Malik. Contour detection and hierarchical image segmentation. Transactions on Pattern Analysis and Machine Intelligence, 33(5):898–916, 2011
- [6] N. Silberman, D. Hoiem, P. Kohli, R. Fergus. Indoor segmentation and support inference from RGBD images. European Conference on Computer Vision, pages 746–760, 2012.
- [7] X. Ren, J. Malik. Learning a classification model for segmentation. International Conference on Computer Vision, pages 10–17, 2003.
- [8] J. Shi, J. Malik. Normalized cuts and image segmentation. Transactions on Pattern Analysis and Machine Intelligence, 22(8):888–905, 2000.
- [9] P. F. Felzenswalb, D. P. Huttenlocher. Efficient graph-based image segmentation. International Journal of Computer Vision, 59(2), 2004.
- [10] A. Vedaldi, S. Soatto. Quick shift and kernel methods for mode seeking. European Conference on Computer Vision, pages 705–718, 2008.
- [11] A. Levinshtein, A. Stere, K. N. Kutulakos, D. J. Fleet, S. J. Dickinson, K. Siddiqi. TurboPixels: Fast superpixels using geometric flows. Transactions on Pattern Analysis and Machine Intelligence, 31(12):2290–2297, 2009.
- [12] C. Rohkohl, K. Engel. Efficient image segmentation using pairwise pixel similarities. Pattern Recognition, volume 4713 of Lecture Notes in Computer Science, pages 254–263, 2007.
- [13] R. Achanta, A. Shaji, K. Smith, A. Lucchi, P. Fua, S. Süsstrunk. SLIC superpixels. Technical report, École Polytechnique Fédérale de Lausanne, 2010.
- [14] O. Veksler, Y. Boykov, P. Mehrani. Superpixels and supervoxels in an energy optimization framework. European Conference on Computer Vision, pages 211–224, 2010.
- [15] M. Y. Lui, O. Tuzel, S. Ramalingam, R. Chellappa. Entropy rate superpixel segmentation. Conference on Computer Vision and Pattern Recognition, pages 2097–2104, 2011.
- [16] Y. Zhang, R. Hartley, J. Mashford, S. Burn. Superpixels via pseudo-boolean optimization. International Conference on Computer Vision, pages 1387–1394, 2011.
- [17] D. Weikersdorfer, D. Gossow, M. Beetz. Depth-adaptive superpixels. International Conference on Pattern Recognition, pages 2087–2090, 2012.
- [18] D. Tang, H. Fu, X. Cao. Topology preserved regular superpixel. International Conference on Multimedia and Expo, pages 765–768, 2012.
- [19] C. Conrad, M. Mertz, R. Mester. Contour-relaxed superpixels. Energy Minimization Methods in Computer Vision and Pattern Recognition, volume 8081 of Lecture Notes in Computer Science, pages 280–293, 2013.
- [20] J. Papon, A. Abramov, M. Schoeler, F. Wörgötter. Voxel cloud connectivity segmentation - supervoxels for point clouds. Conference on Computer Vision and Pattern Recognition, pages 2027–2034, 2013.
- [21] C. Rohkohl, K. Engel. Efficient image segmentation using pairwise pixel similarities. In Pattern Recognition, volume 4713 of Lecture Notes in Computer Science, pages 254–263, 2007.
- [22] A. P. Moore, S. J. D. Prince, J. Warrell, U. Mohammed, G. Jones. Superpixel lattices. Conference on Computer Vision and Pattern Recognition, pages 1–8, 2008.
- [23] F. Drucker, J. MacCormick. Fast superpixels for video analysis. Workshop on Motion and Video Computing, pages 1–8, 2009.
- [24] G. Zeng, P. Wang, J. Wang, R. Gan, H. Zha. Structure-sensitive superpixels via geodesic distance. International Conference on Computer Vision, pages 447–454, 2011.
- [25] F. Perbet, A. Maki. Homogeneous superpixels from random walks. Conference on Machine Vision and Applications, pages 26–30, 2011.
- [26] P. Neubert, P. Protzel. Superpixel benchmark and comparison. Forum Bildverarbeitung, 2012.
- [27] A. Schick, M. Fischer, R. Stiefelhagen. Measuring and evaluating the compactness of superpixels. International Conference on Pattern Recognition, pages 930–934, 2012.